题目内容
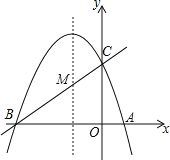
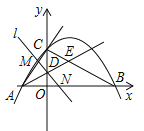
【题目】如图,已知抛物线![]() 与坐标轴交于A,B,C三点,其中C(0,3),∠BAC的平分线AE交y轴于点D,交BC于点E,过点D的直线l与射线AC,AB分别交于点M,N.
与坐标轴交于A,B,C三点,其中C(0,3),∠BAC的平分线AE交y轴于点D,交BC于点E,过点D的直线l与射线AC,AB分别交于点M,N.
(1)直接写出a的值、点A的坐标及抛物线的对称轴;
(2)点P为抛物线的对称轴上一动点,若△PAD为等腰三角形,求出点P的坐标;
(3)证明:当直线l绕点D旋转时,![]() 均为定值,并求出该定值.
均为定值,并求出该定值.
【答案】(1)a=![]() ,A(﹣
,A(﹣![]() ,0),抛物线的对称轴为x=
,0),抛物线的对称轴为x=![]() ;(2)点P的坐标为(
;(2)点P的坐标为(![]() ,2)或(
,2)或(![]() ,0)或(
,0)或(![]() ,﹣4);(3)
,﹣4);(3)![]() .
.
【解析】
试题分析:(1)由点C的坐标为(0,3),可知﹣9a=3,故此可求得a的值,然后令y=0得到关于x的方程,解关于x的方程可得到点A和点B的坐标,最后利用抛物线的对称性可确定出抛物线的对称轴;
(2)利用特殊锐角三角函数值可求得∠CAO=60°,依据AE为∠BAC的角平分线可求得∠DAO=30°,然后利用特殊锐角三角函数值可求得OD=1,则可得到点D的坐标.设点P的坐标为(![]() ,a).依据两点的距离公式可求得AD、AP、DP的长,然后分为AD=PA、AD=DP、AP=DP三种情况列方程求解即可;
,a).依据两点的距离公式可求得AD、AP、DP的长,然后分为AD=PA、AD=DP、AP=DP三种情况列方程求解即可;
(3)设直线MN的解析式为y=kx+1,接下来求得点M和点N的横坐标,于是可得到AN的长,然后利用特殊锐角三角函数值可求得AM的长,最后将AM和AN的长代入化简即可.
试题解析:(1)∵C(0,3),∴﹣9a=3,解得:a=![]() .
.
令y=0得:![]() ,∵a≠0,∴
,∵a≠0,∴![]() ,解得:x=﹣
,解得:x=﹣![]() 或x=
或x=![]() ,∴点A的坐标为(﹣
,∴点A的坐标为(﹣![]() ,0),B(
,0),B(![]() ,0),∴抛物线的对称轴为x=
,0),∴抛物线的对称轴为x=![]() .
.
(2)∵OA=![]() ,OC=3,∴tan∠CAO=
,OC=3,∴tan∠CAO=![]() ,∴∠CAO=60°.
,∴∠CAO=60°.
∵AE为∠BAC的平分线,∴∠DAO=30°,∴DO=![]() AO=1,∴点D的坐标为(0,1).
AO=1,∴点D的坐标为(0,1).
设点P的坐标为(![]() ,a).
,a).
依据两点间的距离公式可知:AD2=4,AP2=12+a2,DP2=3+(a﹣1)2.
当AD=PA时,4=12+a2,方程无解.
当AD=DP时,4=3+(a﹣1)2,解得a=2或a=0,∴点P的坐标为(![]() ,2)或(
,2)或(![]() ,0).
,0).
当AP=DP时,12+a2=3+(a﹣1)2,解得a=﹣4,∴点P的坐标为(![]() ,﹣4).
,﹣4).
综上所述,点P的坐标为(![]() ,2)或(
,2)或(![]() ,0)或(
,0)或(![]() ,﹣4).
,﹣4).
(3)设直线AC的解析式为y=mx+3,将点A的坐标代入得:![]() ,解得:m=
,解得:m=![]() ,∴直线AC的解析式为
,∴直线AC的解析式为![]() .
.
设直线MN的解析式为y=kx+1.
把y=0代入y=kx+1得:kx+1=0,解得:x=![]() ,∴点N的坐标为(
,∴点N的坐标为(![]() ,0),∴AN=
,0),∴AN=![]() =
=![]() .
.
将![]() 与y=kx+1联立解得:x=
与y=kx+1联立解得:x=![]() ,∴点M的横坐标为
,∴点M的横坐标为![]() .
.
过点M作MG⊥x轴,垂足为G.则AG=![]() .
.

∵∠MAG=60°,∠AGM=90°,∴AM=2AG=![]() =
=![]() ,∴
,∴![]() =
=![]() =
=![]() =
=![]() =
=![]() .
.