题目内容
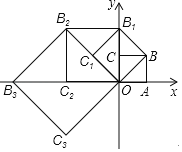
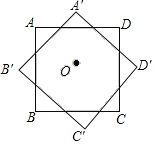
【题目】如图，正方形ABCD的边长为2，点O为其中心．将其绕点O顺时针旋转45°后得到正方形A'B'C'D'，则旋转前后两正方形重叠部分构成的多边形的周长为（ ）（参考计算：
）
A.16﹣8
B.16﹣16C.12﹣8D.16﹣12
【答案】B
【解析】
首先求出正方形的对角线长；进而求出OA′的长；证明△A′MN为等腰直角三角形，求出A′N的长度；同理求出D′M′的长度，即可解决问题．
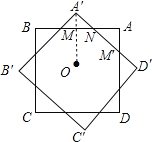
连接OA′，交AB于M，如图所示：
∵正方形ABCD的边长为2，
∴该正方形的对角线长＝2
，
∴OA′＝；而OM＝1，
∴A′M＝﹣1；
由题意得：∠MA′N＝45°，∠A′MN＝90°，
∴∠MNA′＝45°，
∴MN＝A′M＝﹣1；
由勾股定理得：A′N＝2﹣；
同理可求D′M′＝2﹣，
∴NM'＝2﹣（4﹣2）＝2﹣2，
∴正八边形的边长为2﹣2，
故重叠部分构成的多边形的周长为8（2﹣2）＝16﹣16
故选：B．
练习册系列答案
相关题目
【题目】八（2）班组织了一次经典诵读比赛，甲、乙两队各10人的比赛成绩如下表（10分制）：
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
（1）甲队成绩的中位数是 分，乙队成绩的众数是 分；
（2）计算乙队的平均成绩和方差；
（3）已知甲队成绩的方差是1.4，则成绩较为整齐的是 队．
