��Ŀ����
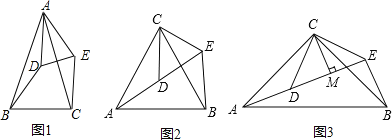
����Ŀ����ͼ1����ABC�ı�BC��ֱ��l�ϣ�AC��BC����AC=BC����EFP�ı�FPҲ��ֱ��l�ϣ���EF���AC�غϣ���EF=FP��
��1��ʾ������ͼ1�У�ͨ���۲졢���������벢д��AB��AP�������������ϵ��λ�ù�ϵ��
��AB��AP��������ϵ��λ�ù�ϵ�ֱ����� ������ ����
��2������EFP��ֱ��l����ƽ�Ƶ�ͼ2��λ��ʱ��EP��AC�ڵ�Q������AP��BQ������۲졢���������벢д��BQ��AP�������������ϵ��λ�ù�ϵ����BQ��AP��������ϵ��λ�ù�ϵ�ֱ����� ������ ����
��3������EFP��ֱ��l����ƽ�Ƶ�ͼ3��λ��ʱ��EP���ӳ��߽�AC���ӳ����ڵ�Q������AP��BQ������Ϊ��2�����������BQ��AP��������ϵ��λ�ù�ϵ��������������������֤����������������˵�����ɣ�
���𰸡���1��AB=AP��AB��AP����2��BQ=AP��BQ��AP����3��������֤���������.
�������������������1������AC��BC����AC=BC����EF���AC�غϣ���EF=FP������ABC����EFP��ȫ�ȵĵ���ֱ�������Σ����ݵ���ֱ�������ε����ʵõ���BAC=��CAP=45����AB=AP������BAP=90��������AP��AB��
��2���ӳ�BO��AP��H�㣬�ɵõ���OPCΪ����ֱ�������Σ�����OC=PC��������SAS�����ж���ACP�ա�BCO����AP=BO����CAP=��CBO�������������ڽǺͶ����ɵõ���AHO=��BCO=90������AP��BO��
��3��BO��AP�������������ϵΪ��ȣ�λ�ù�ϵΪ��ֱ��֤�������루2��һ����
�����������1��AB=AP��AB��AP��
��2��BQ=AP��BQ��AP��
��3���������������£�
�ߡ�EPF=45�������CPQ=45����
��AC��BC�����CQP=��CPQ��CQ=CP��
��Rt��BCQ��Rt��ACP����BC=AC����BCQ=��ACP��CQ=CP����Rt��BCQ��Rt��ACP��SAS����
��BQ=AP��
�ӳ�QB��AP�ڵ�N�����PBN=��CBQ��
��Rt��BCQ��Rt��ACP�����BQC=��APC��
��Rt��BCQ�У��ߡ�BCQ+��CBQ=90�������APC+��PBN=90�������PNB=90������QB��AP��