题目内容
【题目】如图,直线CD与直线AB相交于点C,根据下列语句画图(注:可利用三角尺画图,但要保持图形清晰) 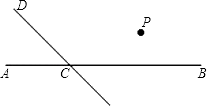
(1)过点P作PQ∥AB,交CD于点Q,过点P作PR⊥CD,垂足为R;
(2)若∠DCB=120°,则∠QRC是多少度?并说明理由.
【答案】
(1)如图,

(2)解:∵PQ∥AB,
∴∠DCB+∠CQP=180°,
∴∠CQP=180°﹣120°=60°,
∵PR⊥CD,
∴∠QPR=90°﹣60°=30°
【解析】(1)利用几何语言画图;(2)根据平行线的性质得到∠CQP=60°,然后利用互余计算∠QPR的度数.
【考点精析】认真审题,首先需要了解垂线的性质(垂线的性质:1、过一点有且只有一条直线与己知直线垂直.2、垂线段最短),还要掌握平行线的性质(两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补)的相关知识才是答题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目