题目内容
在等边△ABC所在平面内有一点P,使得△PBC、△PAC、△PAB都是等腰三角形,则具有该性质的点有( )
| A.1个 | B.7个 | C.10个 | D.无数个 |
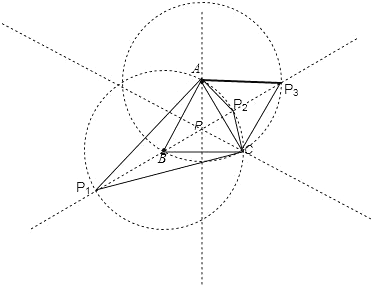
作三边的中垂线,交点P肯定是其中之一,以B为圆心,BA为半径画圆,交AC的中垂线于P1、P2两点,作△P2AB、△P2BC、△P2AC,它们也都是等腰三角形,因此P1、P2是具有题目所说的性质的点;
以A为圆心,BA为半径画圆,交AC的中垂线于点P3、P3也必具有题目所说的性质.
依此类推,在△ABC的其余两条中垂线上也存在这样性质的点,所以这些点一共有:
3×3+1=10个.
故选:C.
以A为圆心,BA为半径画圆,交AC的中垂线于点P3、P3也必具有题目所说的性质.
依此类推,在△ABC的其余两条中垂线上也存在这样性质的点,所以这些点一共有:
3×3+1=10个.

故选:C.

练习册系列答案
相关题目