题目内容
【题目】如图,∠ABC=∠ADC=90°,∠BAD=45°,E、F分别是AC、BD的中点.若AC=2,求EF的长.

【答案】![]() .
.
【解析】
连接BE、DE,利用直角三角形斜边的中线等于斜边的一半证明BED为等腰三角形,再根据外角定理证明∠BED为90°,则△BED为等腰直角三角形,再根据勾股定理即可求出.
连接BE、DE,
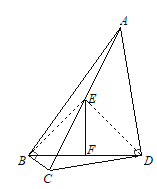
∵∠ABC=∠ADC=90°,E为AC中点,
∴BE=![]() ,DE=
,DE=![]() ,△AEB和△AED是全等三角形.
,△AEB和△AED是全等三角形.
∴∠BEC=2∠BAE,∠DEC=2∠DAE;
∴∠BED=∠BEC+∠DEC=2∠BAE+2∠DAE=2(∠BAE+∠BAE)=2∠BAD=90°;
又∵BE=DE
∴△BED是等腰直角三角形.
∵AC=2,
∴BE=ED=1,
又∵F是BD的中点,
∴EF=![]() .
.

练习册系列答案
相关题目
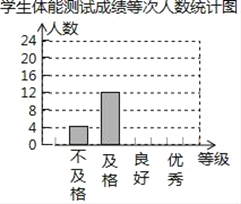
【题目】某校为了解学生体质情况,从各年级随机抽取部分学生进行体能测试,每个学生的测试成绩按标准对应为优秀、良好、及格、不及格四个等级,统计员在将测试数据绘制成图表时发现,优秀漏统计4人,良好漏统计6人,于是及时更正,从而形成如图图表,请按正确数据解答下列各题:
学生体能测试成绩各等次人数统计表
体能等级 | 调整前人数 | 调整后人数 |
优秀 | 8 |
|
良好 | 16 |
|
及格 | 12 |
|
不及格 | 4 |
|
合计 | 40 |
|
(1)填写统计表;
(2)根据调整后数据,补全条形统计图;
(3)若该校共有学生1500人,请你估算出该校体能测试等级为“优秀”的人数.
【题目】已知抛物线y=(x-1)2-1.
(1)该抛物线的对称轴是______________,顶点坐标为____________;
(2)选取适当的数据填入下表,并在图中的直角坐标系内描点画出该抛物线;
x | … | … | |||||
y | … | … |

(3)根据图象,直接写出当y<0时,x的取值范围.





