题目内容
【题目】如图,如图,已知等腰 ABC 中, AC= AB,BD是 ∠ABC 的角平分线.
(1)尺规作图:作出∠ ACB的角平分线,交 AB 于点E , 交BD于点F (不写作法,保留作图痕迹)
(2)试判断 △BFC 的形状,并说明理由.

【答案】见解析
【解析】试题分析:(1)用尺规作图作出∠ACB的平分线即可;
(2)由等腰三角形的性质得到∠ABC=∠ACB,再由角平分线性质得到∠FBC=∠FCB,根据等角对等边即可得到结论.
试题解析:证明:(1)作图
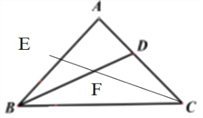
∴如图所示,CE为所求.
(2)△BFC是等腰三角形,理由如下:
∵ AB=AC, ∴∠ABD=∠ACB .
∵BD平分∠ABD,CE平分∠ACB, ∴∠FBC=![]() ∠ABC , ∠FCB=
∠ABC , ∠FCB=![]() ∠ACB, ∴ ∠FBC=∠FCB,∴BF =CF. 即△BFC是等腰三角形.
∠ACB, ∴ ∠FBC=∠FCB,∴BF =CF. 即△BFC是等腰三角形.

练习册系列答案
相关题目
【题目】若干名同学的年龄如表所示:
年龄(岁) | 13 | 14 | 15 |
人数 | 3 | 3 | m |
这些同学的平均年龄是14.4岁,则这些同学年龄的众数和中位数分别是( )
A. 14、14B. 13、14.5C. 15、15D. 14、13.5
【题目】某农场300名职工耕种51公顷土地,计划种植水稻、棉花和蔬菜,已知种植农作物每公顷所需的劳动力人数及投入的设备资金如下表:
农作物品种 | 每公顷需劳动力 | 每公顷需投入资金 |
水稻 | 4人 | 1万元 |
棉花 | 8人 | 1万元 |
蔬菜 | 5人 | 2万元 |
已知该农场计划在设备投入67万元,应该怎样安排这三种作物的种植面积,才能使所有职工有工作,而且投入的资金正好够用?
