题目内容
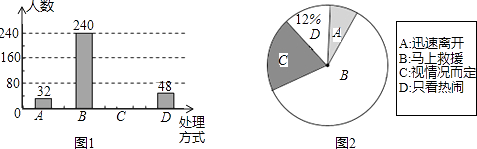
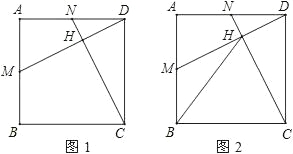
【题目】如图(1),点M、N分别是正方形ABCD的边AB、AD的中点,连接CN、DM.
(1)证明:①CN=DM;②CN⊥DM;
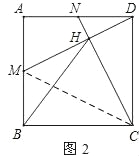
(2)设CN、DM的交点为H,连接BH,如图(2),求证:△BCH是等腰三角形.
【答案】(1)、证明过程见解析;(2)、证明过程见解析
【解析】
试题分析:(1)、利用正方形的性质可求证△ADM≌△DCN,所以CN=DM,∠ADM=∠DCN,∠ADM+∠CDM=∠DCN+∠CDM=90°,即可求证∠CHD=90°;(2)、连接CM,易证M、B、C、H四点共圆,所以∠BMC=∠BHC,证明△AMD≌△BCM,即可求证∠BHC=∠BCH
试题解析:(1)、由题意知:AD=CD, ∵M、N分别是AB和AD的中点, ∴AM=DN,
在△ADM与△DCN中,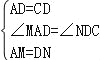 , ∴△ADM≌△DCN(SAS), ∴DM=CN,∠ADM=∠DCN,
, ∴△ADM≌△DCN(SAS), ∴DM=CN,∠ADM=∠DCN,
∴∠DCN+∠CDM=∠ADM+∠CDM=90°, ∴∠CHD=90°, ∴CN⊥DM;
(2)、连接CM, 由(1)可知:∠AMD=90°﹣∠ADM, ∠BCH=90°﹣∠DCN, ∴∠AMD=∠BCH,
∴M、B、C、H四点共圆, ∴∠BMC=∠BHC,
在△BCM与△ADM中,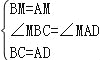 , ∴△BCM≌△ADM(SAS), ∴∠BMC=∠AMD,
, ∴△BCM≌△ADM(SAS), ∴∠BMC=∠AMD,
∴∠BHC=∠AMD=∠BCH, ∴△BCH是等腰三角形

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目