Question

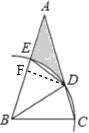
【题目】如图，△ABC中，∠A=30°，AB=AC，以B为圆心，BC长为半径画弧，交AC于点D，交AB于点E.

（1）求∠ABD的度数；

（2）当BC=时，求线段AE，AD与围成阴影部分的面积．

Answer 1

【答案】(1) 45°；(2) .

【解析】

试题分析：（1）根据AB=AC，利用三角形内角和定理求出∠ABC、∠BCD的度数，再利用等腰三角形的性质和三角形内角和定理求出∠DBC=30°，然后即可求出∠ABD的度数；

（2）过点D作DF⊥AB与F，在RT△BDF中和RT△BDF中分别求出DF、BF、AF的长，即可知AB的长，最后根据列式可求得．

试题解析：（1）∵AB=AC，∠A=30°，

∴∠ABC=∠ACB=75°，

∵BC=BD，

∴∠BDC=∠BCD=75°，

∴∠DBC=30°，

∴∠ABD=∠ABC﹣∠DBC=45°；

（2）如图，过点D作DF⊥AB与F，

在RT△BDF中，∠FBD=45°，BD=BC=，

∴BF=DF=BDsin45°=×=1，

在RT△BDF中，∠A=30°，

∴AD=2DF=2，AF=，

∴AB=AF+BF=+1，

∴=ABDF﹣=．