ЬтФПФкШн
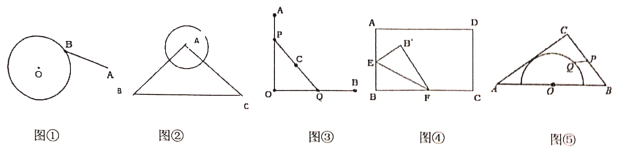
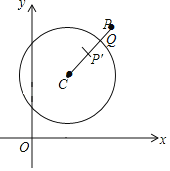
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOy жаЃЌЕуPЪЧЁбCЭтвЛЕуЃЌСЌНгCPНЛЁбCгкЕуQЃЌЕуPЙигкЕуQЕФЖдГЦЕуЮЊPЁфЃЌЕБЕуPЁфдкЯпЖЮCQЩЯЪБЃЌГЦЕуPЮЊЁбCЁАгбКУЕуЁБЃЎвбжЊAЃЈ1ЃЌ0ЃЉЃЌBЃЈ0ЃЌ2ЃЉЃЌCЃЈ3ЃЌ3ЃЉ
ЃЈ1ЃЉЕБЁбOЕФАыОЖЮЊ1ЪБЃЌ
ЂйЕуAЃЌBЃЌCжаЪЧЁбOЁАгбКУЕуЁБЕФЪЧЁЁ ЁЁЃЛ
ЂквбжЊЕуMдкжБЯпyЃНЉ![]() x+2 ЩЯЃЌЧвЕуMЪЧЁбOЁАгбКУЕуЁБЃЌЧѓЕуMЕФКсзјБъmЕФШЁжЕЗЖЮЇЃЛ
x+2 ЩЯЃЌЧвЕуMЪЧЁбOЁАгбКУЕуЁБЃЌЧѓЕуMЕФКсзјБъmЕФШЁжЕЗЖЮЇЃЛ
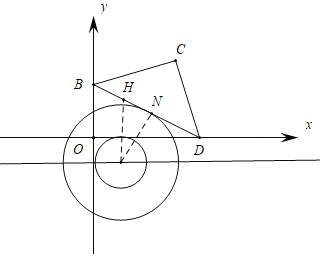
ЃЈ2ЃЉвбжЊЕуD![]() ЃЌСЌНгBCЃЌBDЃЌCDЃЌЁбTЕФдВаФЮЊTЃЈtЃЌЉ1ЃЉЃЌАыОЖЮЊ1ЃЌШєдкЁїBCDЩЯДцдквЛЕуNЃЌЪЙЕуNЪЧЁбTЁАгбКУЕуЁБЃЌЧѓдВаФTЕФКсзјБъtЕФШЁжЕЗЖЮЇЃЎ
ЃЌСЌНгBCЃЌBDЃЌCDЃЌЁбTЕФдВаФЮЊTЃЈtЃЌЉ1ЃЉЃЌАыОЖЮЊ1ЃЌШєдкЁїBCDЩЯДцдквЛЕуNЃЌЪЙЕуNЪЧЁбTЁАгбКУЕуЁБЃЌЧѓдВаФTЕФКсзјБъtЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂйBЃЛЂк0ЁмmЁм![]() ЃЛЃЈ2ЃЉЉ4+3
ЃЛЃЈ2ЃЉЉ4+3![]() ЁмtЃМ3
ЁмtЃМ3![]()
ЁОНтЮіЁП
ЃЈ1ЃЉЃЉЂйИљОнЁАгбКУЕуЁБЕФЖЈвхЃЌOBЃН2rЃН2ЃЌЫљвдЕуBЪЧЁбOЁАгбКУЕуЁБЃЛ
ЂкЩшMЃЈmЃЌЉ![]() m+2 ЃЉЃЌИљОнЁАгбКУЕуЁБЕФЖЈвхЃЌOMЃН
m+2 ЃЉЃЌИљОнЁАгбКУЕуЁБЕФЖЈвхЃЌOMЃН![]()
![]() ЃЌНтЕУ0ЁмmЁм
ЃЌНтЕУ0ЁмmЁм![]() ЃЛ
ЃЛ
ЃЈ2ЃЉBЃЈ0ЃЌ2ЃЉЃЌCЃЈ3ЃЌ3ЃЉЃЌD![]() ЃЌЁбTЕФдВаФЮЊTЃЈtЃЌЉ1ЃЉЃЌЕуNЪЧЁбTЁАгбКУЕуЁБЃЌNTЁм2rЃН2ЃЌЫљвдЕуNжЛФмдкЯпЖЮBDЩЯдЫЖЏЃЌЙ§ЕуTзїTNЁЭBDгкNЃЌзїTHЁЮyжсЃЌгыBDНЛгкЕуHЃЎвзжЊЁЯBDOЃН30ЁуЃЌЁЯOBDЃН60ЁуЃЌNTЃН
ЃЌЁбTЕФдВаФЮЊTЃЈtЃЌЉ1ЃЉЃЌЕуNЪЧЁбTЁАгбКУЕуЁБЃЌNTЁм2rЃН2ЃЌЫљвдЕуNжЛФмдкЯпЖЮBDЩЯдЫЖЏЃЌЙ§ЕуTзїTNЁЭBDгкNЃЌзїTHЁЮyжсЃЌгыBDНЛгкЕуHЃЎвзжЊЁЯBDOЃН30ЁуЃЌЁЯOBDЃН60ЁуЃЌNTЃН![]() HTЃЌжБЯпBDЃКyЃНЉ
HTЃЌжБЯпBDЃКyЃНЉ![]() x+2ЃЌHЃЈtЃЌЉ
x+2ЃЌHЃЈtЃЌЉ![]() t+2 ЩЯЃЉЃЌHTЃНЉ
t+2 ЩЯЃЉЃЌHTЃНЉ![]() t+2ЉЃЈЉ1ЃЉЃНЉ
t+2ЉЃЈЉ1ЃЉЃНЉ![]() t+3ЃЌNTЃН
t+3ЃЌNTЃН![]() HTЃН
HTЃН![]() ЃЈЉ
ЃЈЉ![]() t+3ЃЉЃНЉ
t+3ЃЉЃНЉ![]() t+
t+![]() ЃЌНтГіtЕФЗЖЮЇЃЎ
ЃЌНтГіtЕФЗЖЮЇЃЎ
НтЃКЃЈ1ЃЉЂйЁпrЃН1
ЁрИљОнЁАгбКУЕуЁБЕФЖЈвхЃЌOBЃН2rЃН2
ЁрЕуBЪЧЁбOЁАгбКУЕуЁБ
OCЃН3![]() >2rЃЌВЛЪЧЁбOЁАгбКУЕуЁБ
>2rЃЌВЛЪЧЁбOЁАгбКУЕуЁБ
AЃЈ1ЃЌ0ЃЉдкЁбOЩЯЃЌВЛЪЧЁбOЁАгбКУЕуЁБ
ЙЪД№АИЮЊBЃЛ
ЂкШчЭМЃЌ
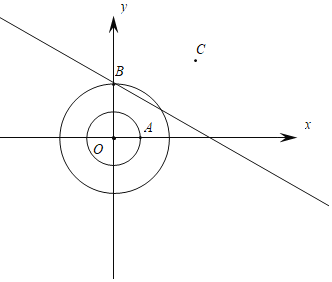
ЩшMЃЈmЃЌЉ![]() m+2 ЃЉЃЌИљОнЁАгбКУЕуЁБЕФЖЈвх
m+2 ЃЉЃЌИљОнЁАгбКУЕуЁБЕФЖЈвх
ЁрOMЃН![]()
ећРэЃЌЕУ2m2Љ2![]() mЁм0
mЁм0
НтЕУ0ЁмmЁм![]() ЃЛ
ЃЛ
ЁрЕуMЕФКсзјБъmЕФШЁжЕЗЖЮЇЃК0ЁмmЁм![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЁпBЃЈ0,2ЃЉ,CЃЈ3,3ЃЉ,D![]() ,ЁбTЕФдВаФЮЊTЃЈt,Љ1ЃЉ,ЕуNЪЧЁбTЁАгбКУЕуЁБ
,ЁбTЕФдВаФЮЊTЃЈt,Љ1ЃЉ,ЕуNЪЧЁбTЁАгбКУЕуЁБ
ЁрNTЁм2rЃН2ЃЌ
ЁрЕуNжЛФмдкЯпЖЮBDЩЯдЫЖЏЃЌЙ§ЕуTзїTNЁЭBDгкNЃЌзїTHЁЮyжсЃЌгыBDНЛгкЕуHЃЎ
взжЊЁЯBDOЃН30ЁуЃЌ
ЁрЁЯOBDЃН60ЁуЃЌ
ЁрNTЃН![]() HTЃЌ
HTЃЌ
ЁпBЃЈ0ЃЌ2ЃЉЃЌD![]() ЃЌ
ЃЌ
ЁржБЯпBDЃКyЃНЉ![]() x+2ЃЌHЃЈtЃЌЉ
x+2ЃЌHЃЈtЃЌЉ![]() t+2 ЩЯЃЉЃЌ
t+2 ЩЯЃЉЃЌ
ЁрHTЃНЉ![]() t+2ЉЃЈЉ1ЃЉЃНЉ
t+2ЉЃЈЉ1ЃЉЃНЉ![]() t+3ЃЌ
t+3ЃЌ
ЁрNTЃН![]() HTЃН
HTЃН![]() ЃЈЉ
ЃЈЉ![]() t+3ЃЉЃНЉ
t+3ЃЉЃНЉ![]() t+
t+![]() ЃЌ
ЃЌ
ЁрЉ![]() t+
t+![]() Ём2ЃЌ
Ём2ЃЌ
ЁрtЁнЉ4+![]() ЃЌ
ЃЌ
ЕБHгыЕуDжиКЯЪБЃЌЕуTЕФКсзјБъЕШгкЕуDЕФКсзјБъЃЌМДtЃН![]() ЃЌ
ЃЌ
ДЫЪБЕуNВЛЪЧЁАгбКУЕуЁБЃЌ
ЁрtЃМ![]() ЃЌ
ЃЌ
ЙЪдВаФTЕФКсзјБъtЕФШЁжЕЗЖЮЇЃКЉ4+![]() ЁмtЃМ
ЁмtЃМ![]() ЃЎ
ЃЎ