题目内容
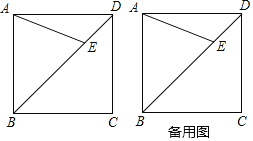
【题目】如图,已知正方形ABCD的边长为3,E是对角线BD上一点(BE>DE).
(1)利用直尺和圆规,在图中过点E作AE的垂线,交BC边于点F(保留作图痕迹,不写作法);
(2)在(1)中,求证:AE=EF;
(3)若(1)中四边形ABFE的面积为4,求AE的长.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)过点E作AE的垂线即可;
(2)如图,过点E作EM⊥AB、EN⊥BC,先证明矩形MBNE是正方形,则∠AEM=∠FEN,再证明△AEM≌△FEN,从而得到AE=EF;
(3)利用△AEM≌△FEN得到S△AEM=S△FEN,则S四边形ABFE=S正方形MBNE,利用正方形面积公式得到BM=2,则AM=AB﹣BM=1,然后利用勾股定理计算AE的长.
(1)如图,

(2)如图,过点E作EM⊥AB、EN⊥BC,
∴∠EMB=∠MBN=∠ENB=90°,
∴四边形MBNE是矩形,
又∵四边形ABCD为正方形,
∴BD平分∠ABC,∴EM=EN,
∴矩形MBNE是正方形,
∵∠AEM+∠MEF=∠MEF+∠FEN=90°,
∴∠AEM=∠FEN,
又∵∠AME=∠FNE=90°,EM=EN,
∴△AEM≌△FEN(ASA),
∴AE=EF;
(3)∵△AEM≌△FEN,
∴S△AEM=S△FEN,
∴S四边形ABFE=S正方形MBNE,
∵四边形ABFE的面积为4,
∴BM2=4,
∴BM=2(取正舍负),
∴AM=AB﹣BM=1,
∴AE=![]()

 阅读快车系列答案
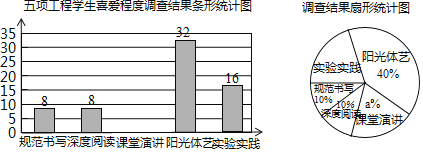
阅读快车系列答案【题目】某校为了解高一年级住校生在校期间的月生活支出情况,从高一年级600名住校学生中随机抽取部分学生,对他们今年4月份的生活支出情况进行调查统计,并绘制成如下统计图表:
组别 | 月生活支出x(单位:元) | 频数(人数) | 频率 |
第一组 | x<300 | 4 | 0.10 |
第二组 | 300≤x<350 | 2 | 0.05 |
第三组 | 350≤x<400 | 16 | n |
第四组 | 400≤x<450 | m | 0.30 |
第五组 | 450≤x<500 | 4 | 0.10 |
第六组 | x≥500 | 2 | 0.05 |
请根据图表中所给的信息,解答下列问题:
(1)在这次调查中共随机抽取了 名学生,图表中的m= ,n ;
(2)请估计该校高一年级600名住校学生今年4月份生活支出低于350元的学生人数;
(3)现有一些爱心人士有意愿资助该校家庭困难的学生,学校在本次调查的基础上,经过进一步核实,确认高一(2)班有A,B,C三名学生家庭困难,其中A,B为女生,C为男生.李阿姨申请资助他们中的两名,于是学校让李阿姨从A,B,C三名学生中依次随机抽取两名学生进行资助,请用列表法(或树状图法)求恰好抽到A,B两名女生的概率.