题目内容
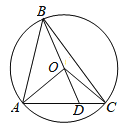
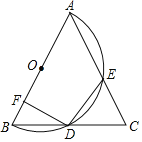
【题目】如图,在△ABC中,AB=AC,以AB为直径作半圆O,交BC于点D,交AC于点E.
(1)求证:BD=CD.
(2)若弧DE=50°,求∠C的度数.
(3)过点D作DF⊥AB于点F,若BC=8,AF=3BF,求弧BD的长.
【答案】(1)详见解析;(2)65°;(3)![]() .
.
【解析】
(1)连接AD,利用圆周角定理推知AD⊥BD,然后由等腰三角形的性质证得结论;
(2)根据已知条件得到∠EOD=50°,结合圆周角定理求得∠DAC=25°,所以根据三角形内角和定理求得∠ABD的度数,则∠C=∠ABD,得解;
(3)设半径OD=x.则AB=2x.由AF=3BF可得AF=![]() AB=
AB=![]() x,BF=
x,BF=![]() AB=
AB=![]() x,根据射影定理知:BD2=BFAB,据此列出方程求得x的值,最后代入弧长公式求解.
x,根据射影定理知:BD2=BFAB,据此列出方程求得x的值,最后代入弧长公式求解.
(1)证明:如图,连接AD.
∵AB是圆O的直径,
∴AD⊥BD.
又∵AB=AC,
∴BD=CD.
(2)解:∵弧DE=50°,
∴∠EOD=50°.
∴∠DAE=![]() ∠DOE=25°.
∠DOE=25°.
∵由(1)知,AD⊥BD,则∠ADB=90°,
∴∠ABD=90°﹣25°=65°.
∵AB=AC,
∴∠C=∠ABD=65°.
(3)∵BC=8,BD=CD,
∴BD=4.
设半径OD=x.则AB=2x.
由AF=3BF可得AF=![]() AB=
AB=![]() x,BF=
x,BF=![]() AB=
AB=![]() x,
x,
∵AD⊥BD,DF⊥AB,
∴BD2=BFAB,即42=![]() x2x.
x2x.
解得x=4.
∴OB=OD=BD=4,
∴△OBD是等边三角形,
∴∠BOD=60°.
∴弧BD的长是:![]() =
=![]() .
.


练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目