题目内容
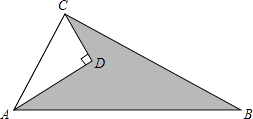
【题目】如图1,在△ABC中,以AB为直径作⊙O分别交AC,BC于点D,E,且![]()

(1)求证:AB=AC.
(2)若∠C=70°,求![]() 的度数.
的度数.
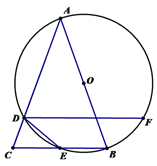
(3)如图2,点F在⊙O上, ![]() ,连结DF,DE.求证:∠ADF=∠CDE.
,连结DF,DE.求证:∠ADF=∠CDE.

【答案】(1)证明见解析(2)100°(3)证明见解析
【解析】(1)连接AE,由圆周角定理得∠AEB=90°,再证⊿AEC≌⊿AEB即可得出AC=AB;(2)利用两弧的差即可求得弧AD![]() 的度数;(3) 利用等弧所对的圆周角相等,圆内接四边形的性质即可求得.
的度数;(3) 利用等弧所对的圆周角相等,圆内接四边形的性质即可求得.
解:(1)连结AE,
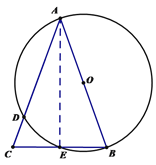
∵AB是直径,
∴∠AEB=900=∠AEC ,
∵弧DE=弧EB![]() ,
,
∴∠CAE=∠EAB,
又∵AE=AE,
∴⊿AEC≌⊿AEB,
∴AC=AB.
(2)∵AB=AC,
∴∠B=∠C=700,
∴∠DAB=400,
∴![]() 弧DB=2∠DAB=800 ,
弧DB=2∠DAB=800 ,
又∵AB是直径,
∴弧ADB![]() =1800,
=1800,
∴弧AD= 弧ADB -弧DB ![]() =1000 .
=1000 .
(3)∵弧BF=弧EB![]() ,AB为直径,
,AB为直径,
∴弧ADB=弧AFB=1800,
∴ 弧AF=弧AE, ![]()
∴∠ADF=∠B ,
又∵四边形ABED内接于圆O,
∴∠CDE=∠B,
∴∠ADF=∠CDE.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目