Question

【题目】已知，△ABC为⊙O的内接等腰三角形，底边AB为，⊙O的半径为4，则∠C度数为___.

Answer 1

【答案】600或1200

【解析】过圆心作AB的垂线，在构建的直角三角形中，易求得圆心角∠AOB的度数，由此可求出∠C的度数.（注意∠C所对的弧可能是优弧，也可能是劣弧）

解：如图，连接OA、OB，过O作OD⊥于AB于D.

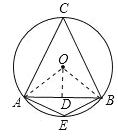
在Rt△OAD中，D=，OA=2，

∴sin∠AOD==，

∴∠AOD=60°，∠AOB=120°.

点C的位置有两种情况：

①当点C在如图位置时，∠C=∠AOB=60°；

②当点C在E点位置时，∠C=∠E=180°-∠F=120°.

故答案为：600或1200.

“点睛”本题主要考查了垂径定理以及解直角三角形的应用，注意点C的位置有两种情况，不要漏解.