题目内容
【题目】在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 上一点.
上一点.
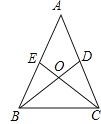
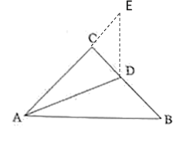
(1)如图![]() ,
,![]() 平分
平分![]() .求证:
.求证:![]() ;
;
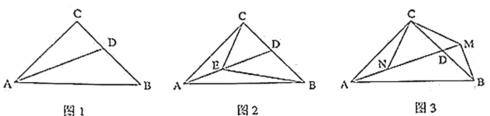
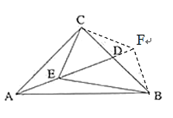
(2)如图![]() ,点
,点![]() 在线段
在线段![]() 上,且
上,且![]() ,
,![]() ,求证:
,求证:![]() .
.
(3)如图![]() ,
,![]() ,过
,过![]() 点作
点作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,过
,过![]() 点作
点作![]() 交
交![]() 于
于![]() ,求证:
,求证:![]() .
.
【答案】(1)见解析;(2)见解析;(3)见解析
【解析】
(1)延长AC至E,使CE=CD,利用AAS证出△BAD≌△EAD,从而得出AB=AE,即可证出结论;
(2)过点C作CF⊥EC交AD的延长线于点F,连接BF,先利用SAS证出△ACE≌△BCF,从而证出AE=BF,∠CEA=∠CFB,再证出∠EFB=90°,利用30°所对的直角边是斜边的一半即可证出结论;
(3)过点C作CE⊥AM于M,先利用AAS证出△CNA≌△CMB,即可证出CN=CM,根据等腰三角形的性质可得NE=EM,然后利用AAS证出△CED≌△BMD,从而得出ED=DM,然后根据线段的关系即可得出结论.
解:(1)延长AC至E,使CE=CD
∵![]() ,
,![]()
∴∠ECD=180°-∠ACB=90°,∠B=∠CAB=![]() (180°-∠ACB)=45°
(180°-∠ACB)=45°
∴△CDE为等腰三角形
∴∠E=45°
∴∠B=∠E
∵![]() 平分
平分![]()
∴∠BAD=∠EAD
在△BAD和△EAD中
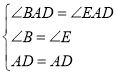
∴△BAD≌△EAD
∴AB=AE
∵AE=AC+CE=AC+CD
∴AB= AC+CD
(2)过点C作CF⊥EC交AD的延长线于点F,连接BF
∵∠CED=45°
∴△CEF为等腰直角三角形
∴CE=CF,∠CFE=∠CEF=45°
∵△ABC为等腰直角三角形
∴∠ACB=90°,CA=CB,
∴∠ACE+∠ECB=90°,∠BCF+∠ECB=90°
∴∠ACE=∠BCF
在△ACE和△BCF中
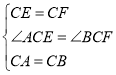
∴△ACE≌△BCF
∴AE=BF,∠CEA=∠CFB
∵∠CEA=180°-∠CEF=135°
∴∠CFB=135°
∴∠EFB=∠CFB-∠CFE=90°
在Rt△EFB中,∠BEF=30°
∴BE=2BF
∴BE=2AE
(3)过点C作CE⊥AM于M,
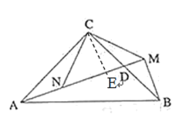
∵△ABC为等腰直角三角形
∴∠ACB=90°,CA=CB
∵CN⊥CM,BM⊥AM
∴∠NCM=90°,∠BMA=90°
∴∠ACN+∠NCB=90°,∠BCM+∠NCB=90°,
∴∠ACN=∠BCM
∴∠CNA=∠NCM+∠CMN=90°+∠CMN=∠CMB
在△CNA和△CMB中
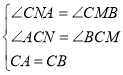
∴△CNA≌△CMB
∴CN=CM
∴△CNM为等腰直角三角形
∴NE=EM
在△CED和△BMD中
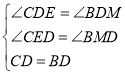
∴△CED≌△BMD
∴ED=DM
∴EM=2DM
∴NE=2DM
∴DN=NE+ED=3DM