Question

【题目】已知线段，为的中点， 为上一点，连接交于点．

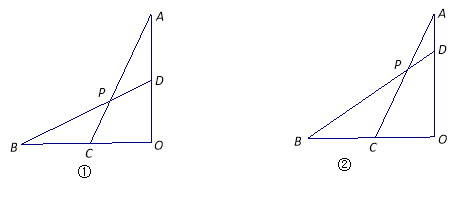
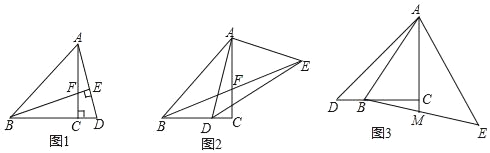
（1）如图，当OA=OB且为中点时，求的值；

（2）如图，当OA=OB，=时，求tan∠．

Answer 1

【答案】（1）2（2）．

【解析】

试题分析：（1）过点作∥交于点E，得出△∽△．然后根据∥得△∽△，从而得出；（2）过点作∥交于点E，设AD=x，然后利用相似三角形的性质得出，，利用勾股定理得出，然后可得∠∠∠，然后求tan∠即可．

试题解析：（1）过点作∥交于点E，则△∽△．

又为的中点，所以，所以．

再由∥得△∽△，所以．

（2）过点作∥交于点E，设AD=x，则，OD=3x．

由△∽△BOD，得．

再由△∽△DAP，得．

由勾股定理可知BD=5x，，则，可得，

则∠∠∠，所以tan∠tan∠=．