Question

【题目】有一直角三角形两直角边分别为6、8，在其外部拼上一个以8为直角边的直角三角形，此时变成等腰三角形，则该等腰三角形的周长是__________．

Answer 1

【答案】32或20+或

【解析】

根据勾股定理求出斜边AB，（1）当AB=AD时，求出CD即可；（2）当AB=BD时，求出CD、AD即可；（3）当DA=DB时，设AD=x，则CD=x-6，求出即可．

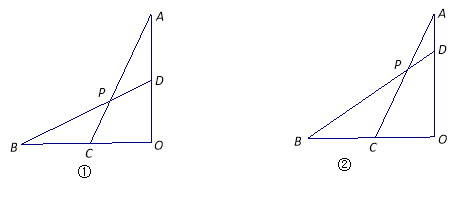
如图1，在Rt△ABC中，

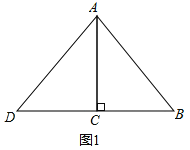
∵AC=8cm，BC=6cm，
∴AB=10cm，
（1）如图1所示：
当AB=AD=10cm时，CD=6cm，
△ABD的周长为10cm+10cm+6cm+6cm=32cm；
（2）如图2所示：

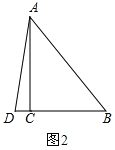
当AB=BD=10cm时，则CD=BD-BC=10-6=4(cm)，

∴(cm)，
△ABD的周长是10cm+10cm+cm=(20+)cm；
（3）当DA=DB时，如图2所示：
设，则，

∴，即，

解得：，

∴△ABD的周长是10cm+cm+cm=cm．

故答案为：32或20+或