题目内容

【题目】如图，在ABCD中，G是CD上一点，连接BG且延长交AD的延长线于点E，AF=CG，∠E=30°，∠C=50°，求∠BFD的度数．

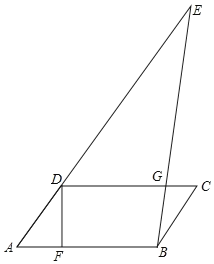
【答案】80°．

【解析】

先根据平行四边形的性质和三角形的内角和定理求出∠ABC与∠ABE度数，据此得出∠CBG度数，再证△BCG≌△DAF得出∠ADF＝∠CBG，继而由三角形外角性质可得答案．

∵四边形ABCD是平行四边形，∠C=50，

∴∠A=∠C=50，∠ABC=180﹣∠C=130，AD=BC．

∵∠E=30，

∴∠ABE=180﹣∠A﹣∠E=100，

∴∠CBG=30，

在△BCG和△DAF中，

∵，

∴△BCG≌△DAF（SAS），

∴∠CBG=∠ADF=30，

则∠BFD=∠A+∠ADF=80．

练习册系列答案
相关题目

【题目】如图，将圆形转盘三等分，分别标上1、2、3三个数字，代表鸡、猴、鼠三种生肖邮票（每种邮票各两枚，鸡年邮票面值“0.80元”，其它邮票都是面值“1.20元”），转动转盘后，指针每落在某个数字所在扇形一次就表示获得该种邮票一枚．

（1）任意转动转盘一次，获得鸡年邮票的概率是　 　；

（2）任意转动转盘两次，求获得的两枚邮票可以邮寄一封需2.4元邮资的信件的概率．

【题目】如图，C为线段AE上一动点（不与A、E重合），在AE同侧分别作正三角形ABC和正三角形CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连结PQ，以下五个结论：①AD=BE；②PQ∥AE；③AP=BQ；④DE=DP；⑤∠AOB=60°其中完全正确的是（ ）

A.①②③④B.②③④⑤C.①③④⑤D.①②③⑤

【题目】如图，△ABC三个顶点的坐标分别为A(1，1)，B(4，2)，C(3，4)．

(1)请画出△ABC向左平移6个单位长度后得到的△A1B1C1；

(2)请画出△ABC关于原点对称的△A2B2C2；

(3)P为x轴上一动点，当AP+CP有最小值时，求这个最小值．

【题目】甲班56人，其中身高在160厘米以上的男同学10人，身高在160厘米以上的女同学3人，乙班80人，其中身高在160厘米以上的男同学20人，身高在160厘米以上的女同学8人．如果想在两个班的160厘米以上的女生中抽出一个作为旗手，在哪个班成功的机会大？为什么？

【题目】（1）如图1，O是等边△ABC内一点，连接OA、OB、OC，且OA=3，OB=4，OC=5，将△BAO绕点B顺时针旋转后得到△BCD，连接OD．求：

①旋转角的度数；

②线段OD的长；

③∠BDC的度数．

（2）如图2所示，O是等腰直角△ABC（∠ABC=90°）内一点，连接OA、OB、OC，将△BAO绕点B顺时针旋转后得到△BCD，连接OD．当OA、OB、OC满足什么条件时，∠ODC=90°？请给出证明．

【题目】已知线段，为的中点， 为上一点，连接交于点．

（1）如图，当OA=OB且为中点时，求的值；

（2）如图，当OA=OB，=时，求tan∠．

【题目】直角三角形的判定

（1）有一个角是________________的三角形是直角三角形．

（2）有两个角________________的三角形是直角三角形．

（3）勾股定理的逆定理：如果三角形两边的平方和等于________________，那么这个三角形是直角三角形．

（4）如果三角形一边上的________________等于这边的一半，那么这个三角形是直角三角形．

【题目】如图，在△ABC中，CD是AB边上的中线，E是CD的中点，过点C作AB的平行线交AE的延长线于点F，连接BF．

(1) 求证：CF＝AD；

(2) 若CA＝CB，∠ACB＝90°，试判断四边形CDBF的形状，并说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网