题目内容
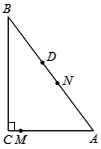
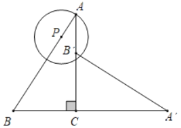
【题目】如图,△ABC中,∠ACB=90°,BC=3,cos∠B=![]() ,将△ABC绕点C顺时针旋转90°得到△AB'C,P为线段AB上的动点,以点P为圆心,PA长为半径作⊙P,当⊙P与△A′B′C的一边所在的直线相切时,⊙P的半径为_____.
,将△ABC绕点C顺时针旋转90°得到△AB'C,P为线段AB上的动点,以点P为圆心,PA长为半径作⊙P,当⊙P与△A′B′C的一边所在的直线相切时,⊙P的半径为_____.
【答案】![]() 或
或![]()
【解析】
分⊙P与△A′B′C的A′B′边、A′C边所在的直线相切两种情况进行讨论即可求得答案.
①当⊙P与△A′B′C的A′B′边所在的直线相切时,即:⊙P′所在的位置,
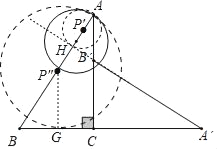
设切点为H点,圆的半径为R,
BC=3,cos∠B=![]() ,则sin∠B=
,则sin∠B=![]() =sin∠AB′H,
=sin∠AB′H,
则AC=A′C=4,BC=CB′=3,AB′=AC﹣B′C=1,
sin∠AB′H=![]() =
=![]() ,则R=
,则R=![]() ;
;
②当⊙P与△A′B′C的A′C边所在的直线相切时,即:⊙P′′所在的位置,
同理,可得:R=![]() ,
,
故答案为:![]() 或
或![]() .
.

练习册系列答案
相关题目