题目内容
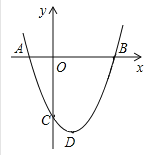
【题目】抛物线 y=ax2+bx+5 的顶点坐标为(2,9),与 y 轴交于点 A(0,5),与 x 轴交于点 E、B(点 E 在点 B 的左侧),点 P 为拋物线上一点.
(1)求该抛物线的解析式;
(2)过点 A 作 AC 平行于 x 轴,交抛物线于点 C,当点 P 在 AC 上方时,作 PD平行于 y 轴交 AB 于点 D,求使四边形 APCD 的面积最大时点 P 的坐标;
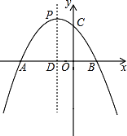
(3)设 N 为 x 轴上一点,当以 A、E、N、P 为顶点,AE 为一边的四边形是平行四边形时,求点 P 的坐标.
【答案】(1)y=﹣x2+4x+5;(2)使四边形 APCD 的面积最大时点 P 的坐标为(![]() );(3)点 P 的坐标(4,5)或P(2
);(3)点 P 的坐标(4,5)或P(2![]() ,﹣5)或(2
,﹣5)或(2![]() ,﹣5).
,﹣5).
【解析】
(1)根据顶点式设出抛物线解析式,用待定系数法求解即可;
(2)先求出直线AB解析式,设出点P坐标(x,﹣x2+4x+5),建立函数关系式S四边形APCD=﹣2x2+10x,根据二次函数求出最值;
(3)分两种情况:
①当P在x轴上方时,以AE为边时,如图2,根据P的纵坐标为5列方程可得P的坐标;
②当P在x轴的下方时,以AE为边,如图3,同理可得P的纵坐标为﹣5,列方程可得P的坐标.
(1)设抛物线解析式为y=a(x﹣2)2+9.
∵抛物线与y轴交于点A(0,5),∴4a+9=5,∴a=﹣1,y=﹣(x﹣2)2+9=﹣x2+4x+5,(2)如图1,当y=0时,﹣x2+4x+5=0,∴x1=﹣1,x2=5,∴E(﹣1,0),B(5,0),设直线AB的解析式为y=mx+n.
∵A(0,5),B(5,0),∴m=﹣1,n=5,∴直线AB的解析式为y=﹣x+5;
设P(x,﹣x2+4x+5).
∵点P在AC上方,∴0<x<4,∴D(x,﹣x+5),∴PD=﹣x2+4x+5+x﹣5=﹣x2+5x.
∵AC=4,∴S四边形APCD=S△APD+S△PCD![]() PDAH
PDAH![]() PDAC
PDAC![]() 4(﹣x2+5x)=﹣2x2+10x=﹣2(x
4(﹣x2+5x)=﹣2x2+10x=﹣2(x![]() )2
)2![]() .
.
∵﹣2<0,∴当x![]() 时,即:使四边形APCD的面积最大时点P的坐标为(
时,即:使四边形APCD的面积最大时点P的坐标为(![]() ).
).
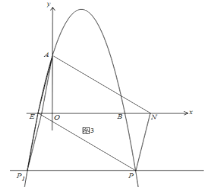
(3)分两种情况:
①当P在x轴上方时,以AE为边时,如图2.
∵N在x轴上,四边形AENP是平行四边形,∴AP∥EN.
∵A(0,5),∴P的纵坐标为5,当y=5时,﹣x2+4x+5=5,解得:x1=0,x2=4,∴P(4,5);

②当P在x轴的下方时,以AE为边,如图3,同理可得P的纵坐标为﹣5,当y=﹣5时,﹣x2+4x+5=﹣5,解得:x=2±![]() ,∴P(2
,∴P(2![]() ,﹣5)或(2
,﹣5)或(2![]() ,﹣5).
,﹣5).
综上所述:点P的坐标(4,5)或(2![]() ,﹣5)或(2
,﹣5)或(2![]() ,﹣5).
,﹣5).

 名校课堂系列答案
名校课堂系列答案