题目内容
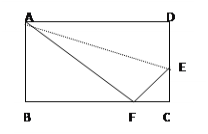
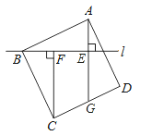
【题目】如图,过正方形ABCD的顶点B作直线l,过点A,C作直线l的垂线,垂足分别为E,F,直线AE交CD于点G.
(1)求证:△ABE≌△BCF;
(2)若∠CBF=65°,求∠AGC的度数.
【答案】(1)证明见解析;(2)115°.
【解析】
试题(1)根据正方形的性质,易得△ABE与△BCF的两角与一条边相等,利用全等三角形的判定条件AAS,可证明两三角形全等;(2)根据△ABE≌△BCF,又知∠CBF=65°,可得∠BAE=65°,又由正方形的性质可得AB∥DC,即可得出∠AGC的度数.
试题解析:解:(1)证明:∵正方形ABCD,

∴AB=CB,∠ABC=90° (1分)
∵AE![]() 于点E,
于点E,
∴∠ABE+∠BAE=90°, (2分)
∴∠BAE=∠CBF. (3分)
又∵∠AEB=∠BFC=90°, (4分)
∴△ABE≌△BCF(AAS). (5分)
(2)∵△ABE≌△BCF,∠CBF=65°,
∴∠BAE=65°, (6分)
又由正方形ABCD得AB∥DC, (7分)
∴∠AGC=115°. (8分)

练习册系列答案
相关题目