题目内容
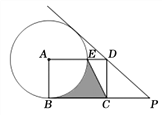
【题目】如图,已知四边形ABCD是矩形,点P在BC边的延长线上,且PD=BC,⊙A经过点B,与AD边交于点E,连接CE .
(1)求证:直线PD是⊙A的切线;
(2)若PC=2![]() ,sin∠P=
,sin∠P=![]() ,求图中阴影部份的面积(结果保留无理数).
,求图中阴影部份的面积(结果保留无理数).
【答案】(1)见解析;(2)20-4π.
【解析】分析:(1)过点A作AH⊥PD,垂足为H,只要证明AH为半径即可.
(2)分别算出Rt△CED的面积,扇形ABE的面积,矩形ABCD的面积即可.
详解:(1)证明:如图,过A作AH⊥PD,垂足为H,
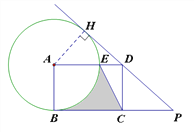
∵四边形ABCD是矩形,
∴AD=BC,AD∥BC,∠PCD=∠BCD=90°,
∴∠ADH=∠P,∠AHD=∠PCD=90°,
又PD=BC,∴AD=PD,
∴△ADH≌△DPC,∴AH=CD,
∵CD=AB,且AB是⊙A的半径,
∴AH=AB,即AH是⊙A的半径,
∴PD是⊙A的切线.
(2)如图,在Rt△PDC中,∵sin∠P=![]() ,PC=2
,PC=2![]() ,
,
令CD=2x,PD=3x,由由勾股定理得:(3x)2-(2x)2=(2![]() )2,
)2,
解得:x=2,∴CD=4,PD=6,
∴AB=AE=CD=4,AD=BC=PD=6,DE=2,
∵矩形ABCD的面积为6×4=24,Rt△CED的面积为![]() ×4×2=4,
×4×2=4,
扇形ABE的面积为![]() π×42=4π,
π×42=4π,
∴图中阴影部份的面积为24-4-4π=20-4π.

练习册系列答案
相关题目