题目内容
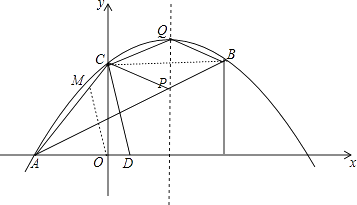
【题目】如图，抛物线y=ax2+bx+4的图象经过A（﹣3，0），B（5，4），与y轴交于点C．
（1）求抛物线的解析式；
（2）线段AB在第一象限内的部分上有一动点P，过点P作y轴的平行线，交抛物线于点Q，是否存在点P使四边形BPCQ的面积最大？如果存在，请求出点P的坐标及面积的最大值；如果不存在，说明理由；
（3）x轴正半轴上有一点D（1，0），线段AC上是否存在点M，使△AOM∽△ADC？如果存在，直接写出点M的坐标；如果不存在，说明理由．
【答案】
（1）
解：根据题意得 
，解得a=﹣ 
，b= 
，
所以抛物线的解析式为y=﹣ x2+ x+4
（2）
解：存在．
如图，设直线AB的解析式为y=mx+n，
把A（﹣3，0），B（5，4）代入得 
，解得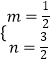 
，
∴直线AB的解析式为y= 
x+ 
，
当x=0时，y=﹣ x2+ x+4=4，则C（0，4），
而B（5，4），
∴BC⊥y轴，
∵QP∥y轴，
∴BC⊥PQ，
设P（t， t+ ）（0＜t＜5），则Q（t，﹣ t2+ t+4），
∴QP=﹣ t2+ t+4﹣ t﹣ t=﹣ t2+ 
t+ 
，
∴S四边形BPCQ=S△CPQ+S△BPQ= PQBC= 5（﹣ t2+ t+ ）
=﹣ 
t2+ 
t+ 
=﹣ （t﹣1）2+ 
，
当t=1时，S四边形BPCQ有最大值，最大值为 ，
此时P点坐标为（1，2）
（3）
解：存在．
直线AC的解析式为y= 
x+4，直线CD的解析式为y=﹣4x+4，
∵△AOM∽△ADC，
∴∠AOM=∠ADC，
∴OM∥CD，
∴直线OM的解析式为y=﹣4x，
解方程组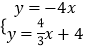 
得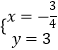 
，
∴M点的坐标为（﹣ 
，3）．
【解析】（1）把A点和B点坐标代入y=ax2+bx+4得到关于a和b的方程组，然后解方程组求出a和b即可得到抛物线解析式；（2）如图，先利用待定系数法求出直线AB的解析式为y= x+ ，则求出C点坐标，从而可判断BC⊥PQ，设P（t， t+ ）（0＜t＜5），则Q（t，﹣ t2+ t+4），再用t表示出QP，然后根据三角形面积公式，利用S四边形BPCQ=S△CPQ+S△BPQ得到S四边形BPCQ=﹣ t2+ t+ ，然后根据二次函数的性质求解；（3）先利用待定系数法求出直线AC的解析式为y= x+4，直线CD的解析式为y=﹣4x+4，则根据相似的性质得到∠AOM=∠ADC，于是可判断OM∥CD，易得直线OM的解析式为y=﹣4x，然后通过解方程组 
可得M点的坐标．
【考点精析】本题主要考查了二次函数的图象和二次函数的性质的相关知识点，需要掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小才能正确解答此题．
