Question

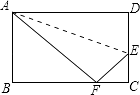
【题目】如图，矩形ABCD中，AB=8，AD=6，点E、F分别在边CD、AB上．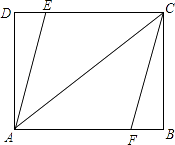

（1）若DE=BF，求证：四边形AFCE是平行四边形；
（2）若四边形AFCE是菱形，求菱形AFCE的周长．

Answer 1

【答案】
（1）解；∵四边形ABCD为矩形，

∴AB=CD，AB∥CD，

∵DE=BF，

∴AF=CE，AF∥CE，

∴四边形AFCE是平行四边形

（2）解；∵四边形AFCE是菱形，

∴AE=CE，

设DE=x，

则AE= ，CE=8﹣x，

则 =8﹣x，

化简有16x﹣28=0，

解得：x= ，

将x= 代入原方程检验可得等式两边相等，

即x= 为方程的解．

则菱形的边长为：8﹣ = ，

周长为：4× =25，

故菱形AFCE的周长为25

【解析】（1）首先根据矩形的性质可得AB平行且等于CD，然后根据DE=BF，可得AF平行且等于CE，即可证明四边形AFCE是平行四边形；（2）根据四边形AFCE是菱形，可得AE=CE，然后设DE=x，表示出AE，CE的长度，根据相等求出x的值，继而可求得菱形的边长及周长．
【考点精析】通过灵活运用平行四边形的判定和菱形的性质，掌握两组对边分别平行的四边形是平行四边形：两组对边分别相等的四边形是平行四边形；一组对边平行且相等的四边形是平行四边形；两组对角分别相等的四边形是平行四边形；对角线互相平分的四边形是平行四边形；菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半即可以解答此题．