��Ŀ����
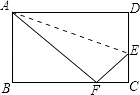
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��A��0��6����B��8��0������P��A���������ÿ��1����λ���ٶ���AO�˶���ͬʱ����Q��O��������ÿ��2����λ���ٶ���OB�˶�����Q�㵽��B��ʱ��P��Q����ͬʱֹͣ�˶���
��1�����˶�ʱ��t��ȡֵ��Χ��
��2�������˶������У��Ե�P��O��QΪ�������������Rt��AOB�м������ƣ���ֱ��д����Ӧ��tֵ��
��3��tΪ��ֵʱ����POQ�����������ֵ�Ƕ��٣�
���𰸡�
��1��
�⣺�ߵ�B������Ϊ��8��0����
��OB=8��
�ߵ�Q��O��������ÿ��2����λ���ٶ���OB�˶�����Q�㵽��B��ʱ��P��Q����ͬʱֹͣ�˶���
��t��4��
���˶�ʱ��t��ȡֵ��ΧΪ��0��t��4
��2��
�⣺������ã�AP=t��OP=6��t��OQ=2t��
�ٵ�Rt��POQ��Rt��AOBʱ�� ![]() =
= ![]() ��
��
�� ![]() =
= ![]() ��
��
��ã�t= ![]() ��
��
�ڵ�Rt��POQ��Rt��BOAʱ�� ![]() =
= ![]() ��
��
�� ![]() =
= ![]() ��
��
��ã�t= ![]() ��
��
��t= ![]() ��
�� ![]() ʱ���Ե�P��O��QΪ�������������Rt��AOB���ƣ�����������
ʱ���Ե�P��O��QΪ�������������Rt��AOB���ƣ�����������
��3��
�⣺��POQ�����= ![]() ��OP��OQ=
��OP��OQ= ![]() ��2t����6��t��=��t2+6t=����t��3��2+9��
��2t����6��t��=��t2+6t=����t��3��2+9��
�൱t=3ʱ����POQ�����������ֵ��9
����������1�������������OB�ij����õ��˶�ʱ��t��ȡֵ��Χ����2����Rt��POQ��Rt��AOB��Rt��POQ��Rt��BOA����������������������ε������г�����ʽ�����㼴�ɣ���3����t��ʾ����POQ����������ݶ��κ��������ʽ�ɣ�
�����㾫����������Ҫ�����˺�����ͼ������֪ʶ�㣬��Ҫ���պ�����ͼ������ֱ������ϵ�е�һϵ�е���ɣ�ͼ����ÿһ�����꣨x��y�������˺�����һ�Զ�Ӧֵ�����ĺ�����x��ʾ�Ա�����ij��ֵ��������y��ʾ������Ӧ�ĺ���ֵ������ȷ�����⣮