题目内容
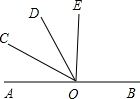
如图,O为直线AB上一点,OC平分∠AOD,OE在∠BOD内,且∠DOE=
∠DOB.若∠COE=72°,求∠DOE的度数.
| 1 |
| 3 |

∵OC平分∠AOD,
∴∠COD=
∠AOD=
(180°-∠DOB),
又∵∠DOE=
∠DOB,
∴∠COE=∠COD+∠DOE=
(180°-∠DOB)+
∠DOB=72°,
解得∠DOB=108°,
∴∠DOE=
∠DOB
×108°=36°.
故答案为:36°.
∴∠COD=
| 1 |
| 2 |
| 1 |
| 2 |
又∵∠DOE=
| 1 |
| 3 |
∴∠COE=∠COD+∠DOE=
| 1 |
| 2 |
| 1 |
| 3 |
解得∠DOB=108°,
∴∠DOE=
| 1 |
| 3 |
| 1 |
| 3 |
故答案为:36°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目