题目内容
【题目】如图,在等腰梯形ABCD中,AD∥BC,AB=DC,AC⊥BD.若AD=4,BC=6,则梯形ABCD的面积是 . 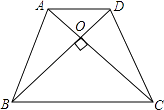
【答案】25
【解析】解:过点D作DE∥AC,交BC的延长线于点E, 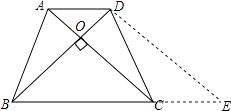
∵AD∥BC,
∴四边形ACED是平行四边形,
∴AC=DE,CE=AD=4,
∴BE=BC+CE=6+4=10,
∵AC⊥BD,
∴DE⊥BD,
∵四边形ABCD是等腰梯形,
∴AC=BD,
∴BD=DE,
∴BD=DE= ![]() =5
=5 ![]() ,
,
∴S梯形ABCD= ![]() ×AC×BD=25.
×AC×BD=25.
所以答案是:25.
【考点精析】本题主要考查了等腰三角形的性质和等腰梯形的性质的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角);等腰梯形的两腰相等;同一底上的两个角相等;两条对角线相等才能正确解答此题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目