题目内容
【题目】如图,在楼房MN前有两棵树与楼房在同一直线上,且垂直于地面,为了测量树AB,CD的高度,小明爬到楼房顶部M处,光线恰好可以经过树CD的顶部C点到达树AB的底部B点,俯角为45°,此时小亮测得太阳光线恰好经过树CD的顶部C点到达楼房的底部N点,与地面的夹角为30°,树CD的影长DN为15米.请求出树AB、CD的高度?(结果保留根号)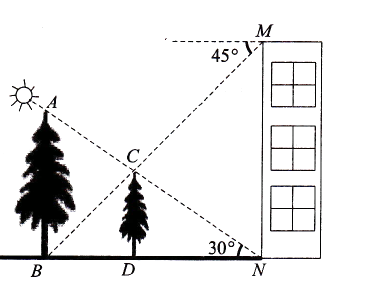
【答案】解:如图,在Rt△CDN中,
∵ tan30°= ![]() ,
,
∴CD=tan30°×DN= ![]() .
.
又∵∠CBD=∠EMB=45°,
∴ BD=CD= ![]() .
.
∴BN=DN+BD=15+ ![]() .
.
在Rt△ABN中,
tan30°= ![]() ,
,
∴AB=tan30°×BN= ![]() ,
,
答:树AB的高度是 ![]() 米;树CD的高度是
米;树CD的高度是 ![]() 米.
米.
【解析】解直角三角形需运用特殊角,及已知边的长度求出一个直角三角形中另外的边长度.
【考点精析】利用特殊角的三角函数值对题目进行判断即可得到答案,需要熟知分母口诀:30度、45度、60度的正弦值、余弦值的分母都是2,30度、45度、60度的正切值、余切值的分母都是3,分子口诀:“123,321,三九二十七”.

练习册系列答案
相关题目
【题目】为降低空气污染,启东飞鹤公交公司决定全部更换节能环保的燃气公交车.计划购买A型和B型两种公交车共10辆,其中每台的价格,年载客量如表:
A型 | B型 | |
价格(万元/台) | a | b |
年载客量(万人/年) | 60 | 100 |
若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求a,b的值;
(2)如果该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次.请你设计一个方案,使得购车总费用最少.