题目内容
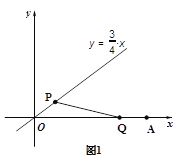
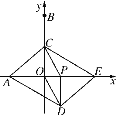
【题目】如图,在平面直角坐标系中,点A,B的坐标分别是(-3,0),(0,6),动点P从点O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C从点B出发,沿射线BO方向以每秒2个单位的速度运动.以CP,CO为邻边构造PCOD.在线段OP延长线上一动点E,且满足PE=AO.
(1)当点C在线段OB上运动时,求证:四边形ADEC为平行四边形;
(2)当点P运动的时间为![]() 秒时,求此时四边形ADEC的周长是多少.
秒时,求此时四边形ADEC的周长是多少.
【答案】(1)证明见解析;(2) 四边形ADEC的周长为6![]() +3
+3![]() .
.
【解析】
(1)连接CD交AE于F,根据平行四边形的性质得到CF=DP,OF=PF,根据题意得到AF=EF,又CF=DP,根据平行四边形的判定定理证明即可;
(2)根据题意计算出OC、OP的长,根据勾股定理求出AC、CE,根据平行四边形的周长公式计算即可.
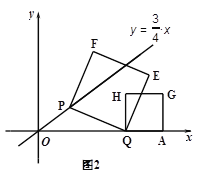
(1)证明:如答图,连接CD交AE于F.
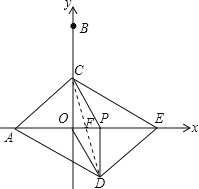
∵四边形PCOD是平行四边形,
∴CF=DF,OF=PF.
∵PE=AO,
∴AF=EF.
又∵CF=DF,
∴四边形ADEC为平行四边形.
(2)解:当点P运动的时间为![]() 秒时,
秒时,
OP=![]() ,OC=3,
,OC=3,
则OE=![]() .
.
由勾股定理,得AC=![]() =3
=3![]() ,
,
CE=![]() =
=![]() .
.
∵四边形ADEC为平行四边形,
∴四边形ADEC的周长为(3![]() +
+![]() )×2=6
)×2=6![]() +3
+3![]() .
.

练习册系列答案
相关题目