Ő‚ńŅńŕ»›
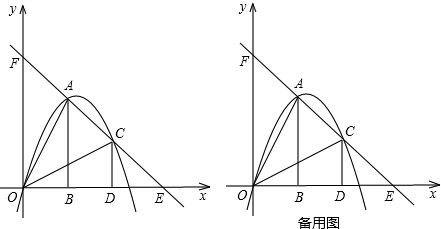
£®2012•Šť÷›£©»ÁÕľ£¨į—ŃĹłŲ»ęĶ»ĶńRt°ųAOBļÕRt°ųCOD∑÷Īū÷√”ŕ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ÷–£¨ Ļ÷ĪĹ«ĪŖOB°ĘOD‘ŕx÷Š…Ō£ģ“—÷™Ķ„A£®1£¨2£©£¨ĻżA°ĘCŃĹĶ„Ķń÷ĪŌŖ∑÷ĪūĹĽx÷Š°Ęy÷Š”ŕĶ„E°ĘF£ģŇ◊őÔŌŖy=ax2+bx+cĺ≠ĻżO°ĘA°ĘC»żĶ„£ģ
£®1£©«ůł√Ň◊őÔŌŖĶńļĮ żĹ‚őŲ Ĺ£Ľ
£®2£©Ķ„Pő™ŌŖ∂őOC…Ō“ĽłŲ∂ĮĶ„£¨ĻżĶ„P◊ųy÷ŠĶń∆Ĺ––ŌŖĹĽŇ◊őÔŌŖ”ŕĶ„M£¨ĹĽx÷Š”ŕĶ„N£¨ő «∑Ůīś‘ŕ’‚—ýĶńĶ„P£¨ ĻĶ√ňńĪŖ–őABPMő™Ķ»—ŁŐ›–ő£Ņ»Űīś‘ŕ£¨«ů≥Ųīň ĪĶ„PĶń◊ÝĪÍ£Ľ»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”…£ģ
£®3£©»Ű°ųAOB—ōAC∑ĹŌÚ∆Ĺ“∆£®Ķ„A ľ÷’‘ŕŌŖ∂őAC…Ō£¨«“≤Ľ”ŽĶ„C÷ōļŌ£©£¨°ųAOB‘ŕ∆Ĺ“∆Ļż≥Ő÷–”Ž°ųCOD÷ōĶĢ≤Ņ∑÷√śĽżľ«ő™S£ģ ‘ŐĹĺŅS «∑Ůīś‘ŕ◊Óīů÷Ķ£Ņ»Űīś‘ŕ£¨«ů≥Ų’‚łŲ◊Óīů÷Ķ£Ľ»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”…£ģ
£®1£©«ůł√Ň◊őÔŌŖĶńļĮ żĹ‚őŲ Ĺ£Ľ
£®2£©Ķ„Pő™ŌŖ∂őOC…Ō“ĽłŲ∂ĮĶ„£¨ĻżĶ„P◊ųy÷ŠĶń∆Ĺ––ŌŖĹĽŇ◊őÔŌŖ”ŕĶ„M£¨ĹĽx÷Š”ŕĶ„N£¨ő «∑Ůīś‘ŕ’‚—ýĶńĶ„P£¨ ĻĶ√ňńĪŖ–őABPMő™Ķ»—ŁŐ›–ő£Ņ»Űīś‘ŕ£¨«ů≥Ųīň ĪĶ„PĶń◊ÝĪÍ£Ľ»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”…£ģ
£®3£©»Ű°ųAOB—ōAC∑ĹŌÚ∆Ĺ“∆£®Ķ„A ľ÷’‘ŕŌŖ∂őAC…Ō£¨«“≤Ľ”ŽĶ„C÷ōļŌ£©£¨°ųAOB‘ŕ∆Ĺ“∆Ļż≥Ő÷–”Ž°ųCOD÷ōĶĢ≤Ņ∑÷√śĽżľ«ő™S£ģ ‘ŐĹĺŅS «∑Ůīś‘ŕ◊Óīů÷Ķ£Ņ»Űīś‘ŕ£¨«ů≥Ų’‚łŲ◊Óīů÷Ķ£Ľ»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”…£ģ

∑÷őŲ£ļ£®1£©Ň◊őÔŌŖy=ax2+bx+cĺ≠ĻżĶ„O°ĘA°ĘC£¨ņŻ”√īż∂®ŌĶ ż∑®«ůŇ◊őÔŌŖĶńĹ‚őŲ Ĺ£Ľ
£®2£©łýĺ›Ķ»—ŁŐ›–őĶń–‘÷ £¨»∑∂®ŌŗĻōĶ„Ķń◊ÝĪÍ“‘ľįŌŖ∂ő≥§∂»Ķń żŃŅĻōŌĶ£¨Ķ√ĶĹ“Ľ‘™∂Ģīő∑Ĺ≥Ő£¨«ů≥ŲtĶń÷Ķ£¨ī”∂ÝŅ…Ĺ‚£ģĹŠ¬Ř£ļīś‘ŕĶ„P£®
£¨
£©£¨ ĻĶ√ňńĪŖ–őABPMő™Ķ»—ŁŐ›–ő£Ľ
£®3£©Īĺő ĻōľŁ ««ůĶ√÷ōĶĢ≤Ņ∑÷√śĽżSĶńĪŪīÔ Ĺ£¨»ĽļůņŻ”√∂ĢīőļĮ żĶńľę÷Ķ«ůĶ√SĶń◊Óīů÷Ķ£ģĹ‚īū÷–ŐŠĻ©Ńň»ż÷÷«ůĹ‚√śĽżSĪŪīÔ ĹĶń∑Ĺ∑®£¨ ‚ÕĺÕ¨Ļť£¨Ņ…◊–ŌłŐŚő∂£ģ
£®2£©łýĺ›Ķ»—ŁŐ›–őĶń–‘÷ £¨»∑∂®ŌŗĻōĶ„Ķń◊ÝĪÍ“‘ľįŌŖ∂ő≥§∂»Ķń żŃŅĻōŌĶ£¨Ķ√ĶĹ“Ľ‘™∂Ģīő∑Ĺ≥Ő£¨«ů≥ŲtĶń÷Ķ£¨ī”∂ÝŅ…Ĺ‚£ģĹŠ¬Ř£ļīś‘ŕĶ„P£®
| 2 |
| 3 |
| 1 |
| 3 |
£®3£©Īĺő ĻōľŁ ««ůĶ√÷ōĶĢ≤Ņ∑÷√śĽżSĶńĪŪīÔ Ĺ£¨»ĽļůņŻ”√∂ĢīőļĮ żĶńľę÷Ķ«ůĶ√SĶń◊Óīů÷Ķ£ģĹ‚īū÷–ŐŠĻ©Ńň»ż÷÷«ůĹ‚√śĽżSĪŪīÔ ĹĶń∑Ĺ∑®£¨ ‚ÕĺÕ¨Ļť£¨Ņ…◊–ŌłŐŚő∂£ģ
Ĺ‚īū£ļĹ‚£ļ£®1£©°ŖŇ◊őÔŌŖy=ax2+bx+cĺ≠ĻżĶ„O°ĘA°ĘC£¨
Ņ…Ķ√c=0£¨°ŗ
£¨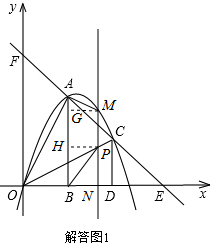
Ĺ‚Ķ√a=-
£¨b=
£¨
°ŗŇ◊őÔŌŖĹ‚őŲ Ĺő™y=-
x2+
x£ģ
£®2£©…ŤĶ„PĶńļŠ◊ÝĪÍő™t£¨°ŖPN°őCD£¨°ŗ°ųOPN°◊°ųOCD£¨Ņ…Ķ√PN=
°ŗP£®t£¨
£©£¨°ŖĶ„M‘ŕŇ◊őÔŌŖ…Ō£¨°ŗM£®t£¨-
t2+
t£©£ģ
»ÁĹ‚īūÕľ1£¨ĻżMĶ„◊ųMG°ÕAB”ŕG£¨ĻżPĶ„◊ųPH°ÕAB”ŕH£¨
AG=yA-yM=2-£®-
t2+
t£©=
t2-
t+2£¨BH=PN=
£ģ
ĶĪAG=BH Ī£¨ňńĪŖ–őABPMő™Ķ»—ŁŐ›–ő£¨
°ŗ
t2-
t+2=
£¨
ĽĮľÚĶ√3t2-8t+4=0£¨Ĺ‚Ķ√t1=2£®≤ĽļŌŐ‚“‚£¨…Š»•£©£¨t2=
£¨
°ŗĶ„PĶń◊ÝĪÍő™£®
£¨
£©
°ŗīś‘ŕĶ„P£®
£¨
£©£¨ ĻĶ√ňńĪŖ–őABPMő™Ķ»—ŁŐ›–ő£ģ
£®3£©»ÁĹ‚īūÕľ2£¨°ųAOB—ōAC∑ĹŌÚ∆Ĺ“∆÷Ń°ųA°šO°šB°š£¨A°šB°šĹĽx÷Š”ŕT£¨ĹĽOC”ŕQ£¨A°šO°šĹĽx÷Š”ŕK£¨ĹĽOC”ŕR£ģ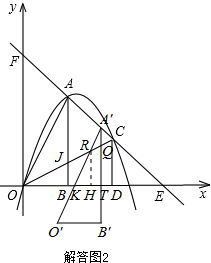
«ůĶ√ĻżA°ĘCĶń÷ĪŌŖő™yAC=-x+3£¨Ņ……ŤĶ„A°šĶńļŠ◊ÝĪÍő™a£¨‘ÚĶ„A°š£®a£¨-a+3£©£¨
“◊÷™°ųOQT°◊°ųOCD£¨Ņ…Ķ√QT=
£¨
°ŗĶ„QĶń◊ÝĪÍő™£®a£¨
£©£ģ
Ĺ‚∑®“Ľ£ļ
…ŤAB”ŽOCŌŗĹĽ”ŕĶ„J£¨
°Ŗ°ųA°šRQ°◊°ųAOJ£¨Ōŗň∆»żĹ«–ő∂‘”¶łŖĶńĪ»Ķ»”ŕŌŗň∆Ī»£¨°ŗ
=
°ŗHT=
•OB=
°Ń1=2-a£¨
KT=
A°šT=
£®3-a£©£¨A°šQ=yA°š-yQ=£®-a+3£©-
=3-
a£ģ
SňńĪŖ–őRKTQ=S°ųA°šKT-S°ųA°šRQ
=
KT•A°šT-
A°šQ•HT
=
•
•£®3-a£©-
•£®3-
a£©•£®-a+2£©
=-
a2+
a-
=-
£®a-
£©2+
”…”ŕ-
£ľ0£¨
°ŗ‘ŕŌŖ∂őAC…Ōīś‘ŕĶ„A°š£®
£¨
£©£¨ń‹ Ļ÷ōĶĢ≤Ņ∑÷√śĽżS»°ĶĹ◊Óīů÷Ķ£¨◊Óīů÷Ķő™
£ģ
Ĺ‚∑®∂Ģ£ļ
ĻżĶ„R◊ųRH°Õx÷Š”ŕH£¨‘Ú”…°ųORH°◊°ųOCD£¨Ķ√
=
=
ĘŔ
”…°ųRKH°◊°ųA°šO°šB°š£¨Ķ√
=
=
Ęŕ
”…ĘŔ£¨ĘŕĶ√KH=
OH£¨
OK=
OH£¨KT=OT-OK=a-
OH ĘŘ
”…°ųA°šKT°◊°ųA°šO°šB°š£¨Ķ√
=
=
£¨
‘ÚKT=
Ę‹
”…ĘŘ£¨Ę‹Ķ√
=a-
OH£¨ľīOH=2a-2£¨RH=a-1£¨ňý“‘Ķ„RĶń◊ÝĪÍő™R£®2a-2£¨a-1£©
SňńĪŖ–őRKTQ=S°ųQOT-S°ųROK=
•OT•QT-
•OK•RH
=
a•
a-
£®1+
a-
£©•£®a-1£©
=-
a2+
a-
=-
£®a-
£©2+
”…”ŕ-
£ľ0£¨
°ŗ‘ŕŌŖ∂őAC…Ōīś‘ŕĶ„A°š£®
£¨
£©£¨ń‹ Ļ÷ōĶĢ≤Ņ∑÷√śĽżS»°ĶĹ◊Óīů÷Ķ£¨◊Óīů÷Ķő™
£ģ
Ĺ‚∑®»ż£ļ
°ŖAB=2£¨OB=1£¨°ŗtan°ŌO°šA°šB°š=tan°ŌOAB=
£¨
°ŗKT=A°šT•tan°ŌO°šA°šB°š=£®-a+3£©•
=-
a+
£¨
°ŗOK=OT-KT=a-£®-
a+
£©=
a-
£¨
ĻżĶ„R◊ųRH°Õx÷Š”ŕH£¨
°Ŗcot°ŌOAB=tan°ŌRKH=
=2£¨
°ŗRH=2KH
”÷°Ŗtan°ŌOAB=tan°ŌROH=
=
=
£¨
°ŗ2RH=OK+KH=
a-
+
RH£¨
°ŗRH=a-1£¨OH=2£®a-1£©£¨
°ŗĶ„R◊ÝĪÍR£®2a-2£¨a-1£©
SňńĪŖ–őRKTQ=S°ųA°šKT-S°ųA°šRQ=
•KT•A°šT-
A°šQ•£®xQ-xR£©
=
•
•£®3-a£©-
•£®3-
a£©•£®-a+2£©
=-
a2+
a-
=-
£®a-
£©2+
”…”ŕ-
£ľ0£¨
°ŗ‘ŕŌŖ∂őAC…Ōīś‘ŕĶ„A°š£®
£¨
£©£¨ń‹ Ļ÷ōĶĢ≤Ņ∑÷√śĽżS»°ĶĹ◊Óīů÷Ķ£¨◊Óīů÷Ķő™
£ģ
Ņ…Ķ√c=0£¨°ŗ
|

Ĺ‚Ķ√a=-
| 3 |
| 2 |
| 7 |
| 2 |
°ŗŇ◊őÔŌŖĹ‚őŲ Ĺő™y=-
| 3 |
| 2 |
| 7 |
| 2 |
£®2£©…ŤĶ„PĶńļŠ◊ÝĪÍő™t£¨°ŖPN°őCD£¨°ŗ°ųOPN°◊°ųOCD£¨Ņ…Ķ√PN=
| t |
| 2 |
°ŗP£®t£¨
| t |
| 2 |
| 3 |
| 2 |
| 7 |
| 2 |
»ÁĹ‚īūÕľ1£¨ĻżMĶ„◊ųMG°ÕAB”ŕG£¨ĻżPĶ„◊ųPH°ÕAB”ŕH£¨
AG=yA-yM=2-£®-
| 3 |
| 2 |
| 7 |
| 2 |
| 3 |
| 2 |
| 7 |
| 2 |
| t |
| 2 |
ĶĪAG=BH Ī£¨ňńĪŖ–őABPMő™Ķ»—ŁŐ›–ő£¨
°ŗ
| 3 |
| 2 |
| 7 |
| 2 |
| t |
| 2 |
ĽĮľÚĶ√3t2-8t+4=0£¨Ĺ‚Ķ√t1=2£®≤ĽļŌŐ‚“‚£¨…Š»•£©£¨t2=
| 2 |
| 3 |
°ŗĶ„PĶń◊ÝĪÍő™£®
| 2 |
| 3 |
| 1 |
| 3 |
°ŗīś‘ŕĶ„P£®
| 2 |
| 3 |
| 1 |
| 3 |
£®3£©»ÁĹ‚īūÕľ2£¨°ųAOB—ōAC∑ĹŌÚ∆Ĺ“∆÷Ń°ųA°šO°šB°š£¨A°šB°šĹĽx÷Š”ŕT£¨ĹĽOC”ŕQ£¨A°šO°šĹĽx÷Š”ŕK£¨ĹĽOC”ŕR£ģ

«ůĶ√ĻżA°ĘCĶń÷ĪŌŖő™yAC=-x+3£¨Ņ……ŤĶ„A°šĶńļŠ◊ÝĪÍő™a£¨‘ÚĶ„A°š£®a£¨-a+3£©£¨
“◊÷™°ųOQT°◊°ųOCD£¨Ņ…Ķ√QT=
| a |
| 2 |
°ŗĶ„QĶń◊ÝĪÍő™£®a£¨
| a |
| 2 |
Ĺ‚∑®“Ľ£ļ
…ŤAB”ŽOCŌŗĹĽ”ŕĶ„J£¨
°Ŗ°ųA°šRQ°◊°ųAOJ£¨Ōŗň∆»żĹ«–ő∂‘”¶łŖĶńĪ»Ķ»”ŕŌŗň∆Ī»£¨°ŗ
| HT |
| OB |
| A°šQ |
| AJ |
°ŗHT=
| A°šQ |
| AJ |
3-a-
| ||
2-
|
KT=
| 1 |
| 2 |
| 1 |
| 2 |
| a |
| 2 |
| 3 |
| 2 |

SňńĪŖ–őRKTQ=S°ųA°šKT-S°ųA°šRQ
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 3-a |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
=-
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 8 |
”…”ŕ-
| 1 |
| 2 |
°ŗ‘ŕŌŖ∂őAC…Ōīś‘ŕĶ„A°š£®
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 8 |
Ĺ‚∑®∂Ģ£ļ
ĻżĶ„R◊ųRH°Õx÷Š”ŕH£¨‘Ú”…°ųORH°◊°ųOCD£¨Ķ√
| RH |
| OH |
| CD |
| OD |
| 1 |
| 2 |

”…°ųRKH°◊°ųA°šO°šB°š£¨Ķ√
| KH |
| RH |
| O°šB°š |
| A°šB°š |
| 1 |
| 2 |
”…ĘŔ£¨ĘŕĶ√KH=
| 1 |
| 4 |
OK=
| 3 |
| 4 |
| 3 |
| 4 |
”…°ųA°šKT°◊°ųA°šO°šB°š£¨Ķ√
| KT |
| A°šT |
| O°šB°š |
| A°šB°š |
| 1 |
| 2 |
‘ÚKT=
| 3-a |
| 2 |
”…ĘŘ£¨Ę‹Ķ√
| 3-a |
| 2 |
| 3 |
| 4 |
SňńĪŖ–őRKTQ=S°ųQOT-S°ųROK=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
=-
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 8 |
”…”ŕ-
| 1 |
| 2 |
°ŗ‘ŕŌŖ∂őAC…Ōīś‘ŕĶ„A°š£®
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 8 |
Ĺ‚∑®»ż£ļ

°ŖAB=2£¨OB=1£¨°ŗtan°ŌO°šA°šB°š=tan°ŌOAB=
| 1 |
| 2 |
°ŗKT=A°šT•tan°ŌO°šA°šB°š=£®-a+3£©•
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
°ŗOK=OT-KT=a-£®-
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
ĻżĶ„R◊ųRH°Õx÷Š”ŕH£¨
°Ŗcot°ŌOAB=tan°ŌRKH=
| RH |
| KH |
°ŗRH=2KH
”÷°Ŗtan°ŌOAB=tan°ŌROH=
| RH |
| OH |
| RH |
| OK+KH |
| 1 |
| 2 |
°ŗ2RH=OK+KH=
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
°ŗRH=a-1£¨OH=2£®a-1£©£¨
°ŗĶ„R◊ÝĪÍR£®2a-2£¨a-1£©
SňńĪŖ–őRKTQ=S°ųA°šKT-S°ųA°šRQ=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 3-a |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
=-
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 8 |
”…”ŕ-
| 1 |
| 2 |
°ŗ‘ŕŌŖ∂őAC…Ōīś‘ŕĶ„A°š£®
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 8 |
Ķ„∆ņ£ļĪĺŐ‚◊ŘļŌŅľ≤ťŃň∂ĢīőļĮ żĶńÕľŌů”Ž–‘÷ °Ęīż∂®ŌĶ ż∑®°Ę∂ĢīőļĮ żĶń◊Ó÷Ķ°ĘĶ»—ŁŐ›–ő°ĘŌŗň∆»żĹ«–ő°ĘÕľ–őĶń∆Ĺ“∆“‘ľįľłļőÕľ–ő√śĽżĶń«ů∑®£¨…śľįĶĹĶń÷™ ∂Ķ„÷ŕ∂ŗ£¨ń—∂»ĹŌīů£¨∂‘—ß…ķń‹Ń¶“™«ůĹŌłŖ£¨”–ņŻ”ŕ—ĶŃ∑≤ĘŐŠ…ż—ß…ķĹ‚ĺŲłī‘”ő Ő‚Ķńń‹Ń¶£ģ

Ń∑Ōį≤ŠŌĶŃ–īūįł
ŌŗĻōŐ‚ńŅ
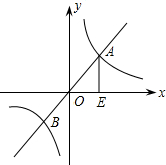 £®2012•Šť÷›£©»ÁÕľ£¨“—÷™ļĮ ży=2xļÕļĮ ż
£®2012•Šť÷›£©»ÁÕľ£¨“—÷™ļĮ ży=2xļÕļĮ ż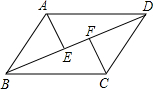 £®2012•Šť÷›£©»ÁÕľ£¨‘ŕ∆Ĺ––ňńĪŖ–őABCD÷–£¨E°ĘF «∂‘Ĺ«ŌŖBD…ŌĶńŃĹĶ„£¨«“BE=DF£¨Ń¨Ĺ”AE°ĘCF£ģ«Žń„≤¬ŌŽ£ļAE”ŽCF”–‘ű—ýĶń żŃŅĻōŌĶ£Ņ≤Ę∂‘ń„Ķń≤¬ŌŽľ”“‘÷§√ų£ģ
£®2012•Šť÷›£©»ÁÕľ£¨‘ŕ∆Ĺ––ňńĪŖ–őABCD÷–£¨E°ĘF «∂‘Ĺ«ŌŖBD…ŌĶńŃĹĶ„£¨«“BE=DF£¨Ń¨Ĺ”AE°ĘCF£ģ«Žń„≤¬ŌŽ£ļAE”ŽCF”–‘ű—ýĶń żŃŅĻōŌĶ£Ņ≤Ę∂‘ń„Ķń≤¬ŌŽľ”“‘÷§√ų£ģ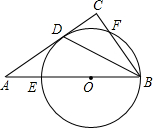 £®2012•Šť÷›£©»ÁÕľ£¨‘ŕRt°ųABC÷–£¨°ŌC=90°„£¨°ŌABCĶń∆Ĺ∑÷ŌŖĹĽAC”ŕĶ„D£¨Ķ„O «AB…Ō“ĽĶ„£¨°—OĻżB°ĘDŃĹĶ„£¨«“∑÷ĪūĹĽAB°ĘBC”ŕĶ„E°ĘF£ģ
£®2012•Šť÷›£©»ÁÕľ£¨‘ŕRt°ųABC÷–£¨°ŌC=90°„£¨°ŌABCĶń∆Ĺ∑÷ŌŖĹĽAC”ŕĶ„D£¨Ķ„O «AB…Ō“ĽĶ„£¨°—OĻżB°ĘDŃĹĶ„£¨«“∑÷ĪūĹĽAB°ĘBC”ŕĶ„E°ĘF£ģ £®2012•Šť÷›£©»ÁÕľ£¨Ķ„A°ĘB°ĘC‘ŕ°—O…Ō£¨°ŌACB=30°„£¨‘Úsin°ŌAOBĶń÷Ķ «£®°°°°£©
£®2012•Šť÷›£©»ÁÕľ£¨Ķ„A°ĘB°ĘC‘ŕ°—O…Ō£¨°ŌACB=30°„£¨‘Úsin°ŌAOBĶń÷Ķ «£®°°°°£©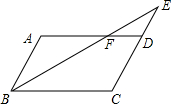 £®2012•Šť÷›£©»ÁÕľ£¨∆Ĺ––ňńĪŖ–őABCD÷–£¨E «CDĶń—”≥§ŌŖ…Ō“ĽĶ„£¨BE”ŽADĹĽ”ŕĶ„F£¨CD=2DE£ģ»Ű°ųDEFĶń√śĽżő™a£¨‘Ú∆Ĺ––ňńĪŖ–őABCDĶń√śĽżő™
£®2012•Šť÷›£©»ÁÕľ£¨∆Ĺ––ňńĪŖ–őABCD÷–£¨E «CDĶń—”≥§ŌŖ…Ō“ĽĶ„£¨BE”ŽADĹĽ”ŕĶ„F£¨CD=2DE£ģ»Ű°ųDEFĶń√śĽżő™a£¨‘Ú∆Ĺ––ňńĪŖ–őABCDĶń√śĽżő™