题目内容
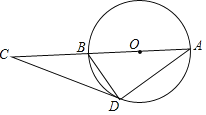
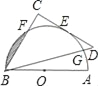
【题目】如图,AB为量角器(半圆O)的直径,等腰直角△BCD的斜边BD交量角器边缘于点G,直角边CD切量角器于读数为60°的点E处(即弧AE的度数为60°),第三边交量角器边缘于点F处.
(1)求量角器在点G处的读数α(90°<α<180°);
(2)若AB=12cm,求阴影部分面积.
【答案】(1)量角器在点G处的读数α=150°;(2)阴影部分的面积为(6π﹣9![]() )cm2.
)cm2.
【解析】
(1)连接OE,OF,则OE⊥CD,由BD为等腰直角△BCD的斜边,则BC⊥CD,从而求得∠D=∠CBD,进而得出∠ABG的度数,则可求得α为150°;
(2)根据已知可得出△OBF为正三角形,则∠BOF=60°,再求得S扇形和S△OBF,从而得出S阴影即可.
连接OE,OF,

(1)∵CD切半圆O于点E,
∴OE⊥CD,
∵BD为等腰直角△BCD的斜边,
∴BC⊥CD,∠D=∠CBD=45°,
∴OE∥BC,
∴∠ABC=∠AOE=60°,
∴∠ABG=∠ABC﹣∠CBD=60°﹣45°=15°,
∴弧AG的度数=2∠ABG=30°,
∴量角器在点G处的读数α=150°;
(2)∵OF=OB=![]() AB=6cm,∠ABC=60°,
AB=6cm,∠ABC=60°,
∴△OBF为正三角形,∠BOF=60°,
∴S扇形=![]() =6π(cm2),S△OBF=
=6π(cm2),S△OBF=![]() ×62=9
×62=9![]() (cm2),
(cm2),
∴S阴影=S扇形﹣S△OBF=(6π﹣9![]() )cm2
)cm2
∴阴影部分的面积为(6π﹣9![]() )cm2.
)cm2.

练习册系列答案
相关题目