题目内容
【题目】在⊙O中,弦AB、CD相交于点E,连接AC、BC,AC=BC,AB=CD. 
(1)如图1,求证:BE平分∠CBD;
(2)如图2,F为BC上一点,连接AF交CD于点G,当∠FAB= ![]() ∠ACB时,求证:AC=BD+2CF;
∠ACB时,求证:AC=BD+2CF;
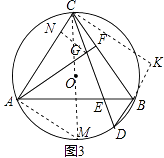
(3)如图3,在(2)的条件下,若S△ACF=S△CBD , ⊙O的半径为3 ![]() ,求线段GD的长.
,求线段GD的长.
【答案】
(1)证明:∵AB=CD,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∵AC=BC,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴∠ABC=∠ABD,
∴BE平分∠CBD
(2)证明:
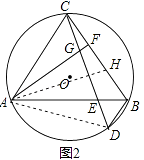
如图2,在线段BF上取点H,使FH=FC,连接AH,AD,
∵AC=BC,∴∠CAB=∠CBA,
∵在△ABC中,∠CAB+∠CBA+∠ACB=180°,
∴∠CBA+ ![]() ∠ACB=90°,
∠ACB=90°,
∵∠FAB= ![]() ∠ACB,
∠ACB,
∴∠FAB+∠CBA=90°,
∴∠AFB=90°,
∴AF⊥CH,
∵CF=FH,
∴AC=AH,
∴∠ACB=∠AHC,
∵A、C、B、D四点在⊙O上,
∴∠ACB+∠ADB=180°,
∵∠AHC+∠AHB=180°,
∴∠AHB=∠ADB,
∵∠ABC=∠ABD,AB=AB,
在△AHB与△ADB中,
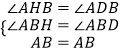 ,
,
∴△AHB≌△ADB,
∴BD=BH,
∵AC=BC=CF+FH+HB,
∴AC=BD+2CF
(3)解:如图3,过点C作CK⊥BD于点K,作直径CM,连接AM,
∵∠CBA=∠CAB=∠ABD,
∴AC∥BD,
∴∠CBK=∠ACB,∠CKB=∠AFC,AC=BC,
在△AFC与△CKB中, 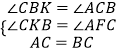 ,
,
∴△AFC≌△CKB,
∴S△AFC=S△CKB=S△CBD,
∴BD=BK=CF,
∵AC=BD+2CF,
∴AC=3CF=3BD,
设BD=CF=k,则AC=BC=3k,BF=2k,
在Rt△ACF中,由勾股定理得:AF=2 ![]() k,
k,
在Rt△AFB中,tan∠FBA= ![]() ,
,
∵CM为⊙O的直径,
∴∠CAM=90°,
∵∠CMA=∠CBA,
在Rt△ACM中,AC=3k,tan∠CMA= ![]() ,CM=6
,CM=6 ![]() ,
,
∴AM= ![]() k,
k,
由勾股定理得:(3k)2+( ![]() )2=(6
)2=(6 ![]() )2,
)2,
∴k=4,
∴AC=12,CF=4,AF=8 ![]() ,
,
在Rt△ACF中,tan∠CAF= ![]() ,tan∠ACD=
,tan∠ACD= ![]() ,AC=12,
,AC=12,
∴CG= ![]() ,
,
在Rt△AFB中,AF=8 ![]() ,FB=8,
,FB=8,
由勾股定理得:AB=CD=8 ![]() ,
,
∴DG= ![]() .
.
【解析】(1)由AB=CD,得到 ![]() =
= ![]() ,由AC=BC,得到
,由AC=BC,得到 ![]() =
= ![]() ,于是得到
,于是得到 ![]() =
= ![]() ,根据圆周角定理即可证得结论.(2)根据全等三角形的性质得到∠CAB=∠CBA,根据三角形的内角和得到∠CBA+
,根据圆周角定理即可证得结论.(2)根据全等三角形的性质得到∠CAB=∠CBA,根据三角形的内角和得到∠CBA+ ![]() ∠ACB=90°推出AF⊥CH,得到∠ACB=∠AHC,根据圆内接四边形的性质得到∠ACB+∠ADB=180°,等量代换得到∠AHB=∠ADB,根据全等三角形的性质得到BD=BH,即可得到结论;(3)根据已知条件得到AC∥BD,根据平行线的性质得到∠CBK=∠ACB,∠CKB=∠AFC,推出△AFC≌△CKB,于是得到S△AFC=S△CKB=S△CBD , 等量代换得到AC=3CF=3BD,设BD=CF=k,则AC=BC=3k,BF=2k,根据勾股定理得到AF=2
∠ACB=90°推出AF⊥CH,得到∠ACB=∠AHC,根据圆内接四边形的性质得到∠ACB+∠ADB=180°,等量代换得到∠AHB=∠ADB,根据全等三角形的性质得到BD=BH,即可得到结论;(3)根据已知条件得到AC∥BD,根据平行线的性质得到∠CBK=∠ACB,∠CKB=∠AFC,推出△AFC≌△CKB,于是得到S△AFC=S△CKB=S△CBD , 等量代换得到AC=3CF=3BD,设BD=CF=k,则AC=BC=3k,BF=2k,根据勾股定理得到AF=2 ![]() k,由圆周角定理得到∠CAM=90°,解直角三角形得到AM=
k,由圆周角定理得到∠CAM=90°,解直角三角形得到AM= ![]() k,根据勾股定理列方程得到AC=12,CF=4,AF=8
k,根据勾股定理列方程得到AC=12,CF=4,AF=8 ![]() ,解直角三角形即可得到结论.
,解直角三角形即可得到结论.

【题目】某商场销售甲、乙两种品牌的智能手机,这两种手机的进价和售价如下表:
甲 | 乙 | |
进价(元/部) | 4000 | 2500 |
售价(元/部) | 4300 | 3000 |
该商场计划购进两种手机若干部,共需15.5万元,预计全部销售后可获毛利润共2.1万元.
(毛利润=(售价﹣进价)×销售量)
(1)该商场计划购进甲、乙两种手机各多少部?
(2)通过市场调研,该商场决定在原计划的基础上,减少甲种手机的购进数量,增加乙种手机的购进数量.已知乙种手机增加的数量是甲种手机减少的数量的2倍,而且用于购进这两种手机的总资金不超过16万元,该商场怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.





