题目内容
【题目】抛物线y=(x﹣3)(x+1)与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,点D为顶点.
(1)求点B及点D的坐标.
(2)连结BD,CD,抛物线的对称轴与x轴交于点E.
①若线段BD上一点P,使∠DCP=∠BDE,求点P的坐标.
②若抛物线上一点M,作MN⊥CD,交直线CD于点N,使∠CMN=∠BDE,求点M的坐标.
【答案】
(1)
解:∵抛物线y=(x﹣3)(x+1)与x轴交于A,B两点(点A在点B左侧),
∴当y=0时,(x﹣3)(x+1)=0,
解得x=3或﹣1,
∴点B的坐标为(3,0).
∵y=(x﹣3)(x+1)=x2﹣2x﹣3=(x﹣1)2﹣4,
∴顶点D的坐标为(1,﹣4)
(2)
解:①如图.

∵抛物线y=(x﹣3)(x+1)=x2﹣2x﹣3与与y轴交于点C,
∴C点坐标为(0,﹣3).
∵对称轴为直线x=1,
∴点E的坐标为(1,0).
连接BC,过点C作CH⊥DE于H,则H点坐标为(1,﹣3),
∴CH=DH=1,
∴∠CDH=∠BCO=∠BCH=45°,
∴CD= ![]() ,CB=3
,CB=3 ![]() ,△BCD为直角三角形.
,△BCD为直角三角形.
分别延长PC、DC,与x轴相交于点Q,R.
∵∠BDE=∠DCP=∠QCR,
∠CDB=∠CDE+∠BDE=45°+∠DCP,
∠QCO=∠RCO+∠QCR=45°+∠DCP,
∴∠CDB=∠QCO,
∴△BCD∽△QOC,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴OQ=3OC=9,即Q(﹣9,0).
∴直线CQ的解析式为y=﹣ ![]() x﹣3,
x﹣3,
直线BD的解析式为y=2x﹣6.
由方程组  ,解得
,解得  .
.
∴点P的坐标为( ![]() ,﹣
,﹣ ![]() );
);
②(Ⅰ)当点M在对称轴右侧时.
若点N在射线CD上,如备用图1,延长MN交y轴于点F,过点M作MG⊥y轴于点G.

∵∠CMN=∠BDE,∠CNM=∠BED=90°,
∴△MCN∽△DBE,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴MN=2CN.
设CN=a,则MN=2a.
∵∠CDE=∠DCF=45°,
∴△CNF,△MGF均为等腰直角三角形,
∴NF=CN=a,CF= ![]() a,
a,
∴MF=MN+NF=3a,
∴MG=FG= ![]() a,
a,
∴CG=FG﹣FC= ![]() a,
a,
∴M( ![]() a,﹣3+
a,﹣3+ ![]() a).
a).
代入抛物线y=(x﹣3)(x+1),解得a= ![]() ,
,
∴M( ![]() ,﹣
,﹣ ![]() );
);
若点N在射线DC上,如备用图2,MN交y轴于点F,过点M作MG⊥y轴于点G.

∵∠CMN=∠BDE,∠CNM=∠BED=90°,
∴△MCN∽△DBE,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴MN=2CN.
设CN=a,则MN=2a.
∵∠CDE=45°,
∴△CNF,△MGF均为等腰直角三角形,
∴NF=CN=a,CF= ![]() a,
a,
∴MF=MN﹣NF=a,
∴MG=FG= ![]() a,
a,
∴CG=FG+FC= ![]() a,
a,
∴M( ![]() a,﹣3+
a,﹣3+ ![]() a).
a).
代入抛物线y=(x﹣3)(x+1),解得a=5 ![]() ,
,
∴M(5,12);
(Ⅱ)当点M在对称轴左侧时.
∵∠CMN=∠BDE<45°,
∴∠MCN>45°,
而抛物线左侧任意一点K,都有∠MCN<45°,
∴点M不存在.
综上可知,点M坐标为( ![]() ,﹣
,﹣ ![]() )或(5, 12).
)或(5, 12).
【解析】(1)解方程(x﹣3)(x+1)=0,求出x=3或﹣1,根据抛物线y=(x﹣3)(x+1)与x轴交于A,B两点(点A在点B左侧),确定点B的坐标为(3,0);将y=(x﹣3)(x+1)配方,写成顶点式为y=x2﹣2x﹣3=(x﹣1)2﹣4,即可确定顶点D的坐标;(2)①根据抛物线y=(x﹣3)(x+1),得到点C、点E的坐标.连接BC,过点C作CH⊥DE于H,由勾股定理得出CD= ![]() ,CB=3
,CB=3 ![]() ,证明△BCD为直角三角形.分别延长PC、DC,与x轴相交于点Q,R.根据两角对应相等的两三角形相似证明△BCD∽△QOC,则
,证明△BCD为直角三角形.分别延长PC、DC,与x轴相交于点Q,R.根据两角对应相等的两三角形相似证明△BCD∽△QOC,则 ![]() =
= ![]() =
= ![]() ,得出Q的坐标(﹣9,0),运用待定系数法求出直线CQ的解析式为y=﹣
,得出Q的坐标(﹣9,0),运用待定系数法求出直线CQ的解析式为y=﹣ ![]() x﹣3,直线BD的解析式为y=2x﹣6,解方程组
x﹣3,直线BD的解析式为y=2x﹣6,解方程组  ,即可求出点P的坐标;②分两种情况进行讨论:(Ⅰ)当点M在对称轴右侧时.若点N在射线CD上,如备用图1,延长MN交y轴于点F,过点M作MG⊥y轴于点G,先证明△MCN∽△DBE,由相似三角形对应边成比例得出MN=2CN.设CN=a,再证明△CNF,△MGF均为等腰直角三角形,然后用含a的代数式表示点M的坐标,将其代入抛物线y=(x﹣3)(x+1),求出a的值,得到点M的坐标;若点N在射线DC上,同理可求出点M的坐标;(Ⅱ)当点M在对称轴左侧时.由于∠BDE<45°,得到∠CMN<45°,根据直角三角形两锐角互余得出∠MCN>45°,而抛物线左侧任意一点K,都有∠MCN<45°,所以点M不存在.
,即可求出点P的坐标;②分两种情况进行讨论:(Ⅰ)当点M在对称轴右侧时.若点N在射线CD上,如备用图1,延长MN交y轴于点F,过点M作MG⊥y轴于点G,先证明△MCN∽△DBE,由相似三角形对应边成比例得出MN=2CN.设CN=a,再证明△CNF,△MGF均为等腰直角三角形,然后用含a的代数式表示点M的坐标,将其代入抛物线y=(x﹣3)(x+1),求出a的值,得到点M的坐标;若点N在射线DC上,同理可求出点M的坐标;(Ⅱ)当点M在对称轴左侧时.由于∠BDE<45°,得到∠CMN<45°,根据直角三角形两锐角互余得出∠MCN>45°,而抛物线左侧任意一点K,都有∠MCN<45°,所以点M不存在.

 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案【题目】如图,伞不论张开还是收紧,伞柄AP始终平分同一平面内两条伞架所成的角∠BAC,当伞收紧时,结点D与点M重合,且点A、E、D在同一条直线上,已知部分伞架的长度如下:单位:cm
伞架 | DE | DF | AE | AF | AB | AC |
长度 | 36 | 36 | 36 | 36 | 86 | 86 |
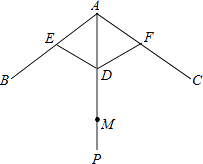
(1)求AM的长.
(2)当∠BAC=104°时,求AD的长(精确到1cm). 备用数据:sin52°=0.788,cos52°=0.6157,tan52°=1.2799.