题目内容
如图,直线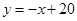 与
与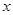 轴、
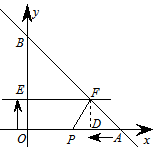
轴、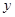 轴分别交于A、B两点,动点P从A点开始在线段AO上以每秒3个长度单位的速度向原点O运动. 动直线EF从
轴分别交于A、B两点,动点P从A点开始在线段AO上以每秒3个长度单位的速度向原点O运动. 动直线EF从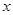 轴开始以每秒1个长度单位的速度向上平行移动(即EF∥
轴开始以每秒1个长度单位的速度向上平行移动(即EF∥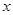 轴),并且分别与
轴),并且分别与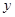 轴、线段AB交于E、F点.连结FP,设动点P与动直线EF同时出发,运动时间为t秒.
轴、线段AB交于E、F点.连结FP,设动点P与动直线EF同时出发,运动时间为t秒.
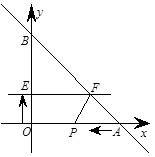
(1)当t=1秒时,求梯形OPFE的面积;
(2)t为何值时,梯形OPFE的面积最大,最大面积是多少?
(3)设t的值分别取t1、t2时(t1≠t2),所对应的三角形分别为△AF1P1和△AF2P2.试判断这两个三角形是否相似,请证明你的判断.
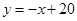 与
与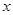 轴、
轴、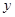 轴分别交于A、B两点,动点P从A点开始在线段AO上以每秒3个长度单位的速度向原点O运动. 动直线EF从
轴分别交于A、B两点,动点P从A点开始在线段AO上以每秒3个长度单位的速度向原点O运动. 动直线EF从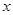 轴开始以每秒1个长度单位的速度向上平行移动(即EF∥
轴开始以每秒1个长度单位的速度向上平行移动(即EF∥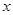 轴),并且分别与
轴),并且分别与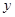 轴、线段AB交于E、F点.连结FP,设动点P与动直线EF同时出发,运动时间为t秒.
轴、线段AB交于E、F点.连结FP,设动点P与动直线EF同时出发,运动时间为t秒.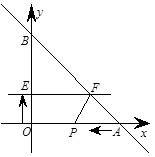
(1)当t=1秒时,求梯形OPFE的面积;
(2)t为何值时,梯形OPFE的面积最大,最大面积是多少?
(3)设t的值分别取t1、t2时(t1≠t2),所对应的三角形分别为△AF1P1和△AF2P2.试判断这两个三角形是否相似,请证明你的判断.
(1)18;(2)50;(3)相似
试题分析:(1)先根据直线的性质求出A、B两点的坐标,再根据点A的移动规律,得到AP的长,从而求出OP的长;又因为EF=BE,用OB的长减去OE的长即可求出EF的长;从而利用梯形面积公式求出梯形OPFE面积;
(2)设OE=t,AP=3t,利用梯形面积公式,将梯形面积转化为关于t的二次函数表达式,求二次函数的最大值即可;
(3)作FD⊥x轴于D,则四边形OEFD为矩形.求出三角形各边的长度表达式,计算出对应边的比值,加上一个夹角相等,即可得到结果.
设梯形OPFE的面积为S.
(1) A(20,0),B(0,20)
∴OA=OB=20,∠A=∠B=45°
当t=1时,OE=1,AP=3
∴OP=17,EF=BE=19
∴S=
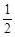 (OP+EF)·OE=18;
(OP+EF)·OE=18;(2) OE=t,AP=3t
∴OP=20-3t,EF=BE=20-t
∴S=
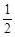 (OP+EF)·OE=
(OP+EF)·OE=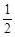 (20-3t +20-t)·t=-2t2+20t=-2(t-5)2+50
(20-3t +20-t)·t=-2t2+20t=-2(t-5)2+50∴当t="5" (在0<t<
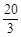 范围内)时,S最大值=50;
范围内)时,S最大值=50;(3) 作FD⊥x轴于D,则四边形OEFD为矩形
∴FD=OE=t,AF=
 FD=
FD= t,又AP=3t
t,又AP=3t当t=t1时,AF1=
 t1,AP1=3t1
t1,AP1=3t1当t=t2时,AF2=
 t2,AP2=3t2
t2,AP2=3t2∴
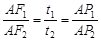 ,又∠A=∠A
,又∠A=∠A∴△AF1P1∽△AF2P2.
点评:解答本题的关键是熟记求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法,常用的是后两种方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
, 分别经过点A(3,0),点B(-1,0),并且当两直线同时相交于y负半轴的点C时,恰好有
分别经过点A(3,0),点B(-1,0),并且当两直线同时相交于y负半轴的点C时,恰好有 ,经过点A、B、C的抛物线的对称轴与直线
,经过点A、B、C的抛物线的对称轴与直线
 绕点C顺时针旋转一个锐角时,它与抛物线的另一个交点为P(x,y),求四边形APCB面积S关于x的函数解析式,并求S的最大值;
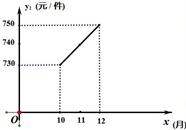
绕点C顺时针旋转一个锐角时,它与抛物线的另一个交点为P(x,y),求四边形APCB面积S关于x的函数解析式,并求S的最大值; 的图象与该二次函数的图象交于A点(8,8),直线与x轴的交点为C,与y轴的交点为B.
的图象与该二次函数的图象交于A点(8,8),直线与x轴的交点为C,与y轴的交点为B.
 不动,而把
不动,而把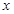 轴、
轴、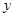 轴分别向上、向右平移3个单位,那么在新坐标系下抛物线的解析式是( )
轴分别向上、向右平移3个单位,那么在新坐标系下抛物线的解析式是( )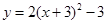
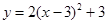
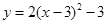

 向右平移1个单位后,得到的抛物线的解析式是 .
向右平移1个单位后,得到的抛物线的解析式是 .
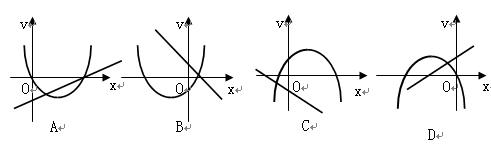
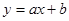 和二次函数
和二次函数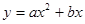 的图象可能为 ( )
的图象可能为 ( )