Question

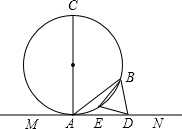已知：如图，AC是⊙O的直径，AB是弦，MN是过点A的直线，AB等于半径长．
（1）若∠BAC=2∠BAN，求证：MN是⊙O的切线．
（2）在（1）成立的条件下，当点E是

AB

的中点时，在AN上截取AD=AB，连接BD、BE、DE，求证：△BED是等边三角形．

Answer 1

分析：（1）连接OB．由AC是⊙O的直径，AB是弦且等于半径长，易证△AOB为等边三角形，得到∠BAC=2∠BAN=60°，得∠BAN=30°，所以∠CAN=∠BAC+∠BAN=90°；
（2）连接AE，由E是弧AB的中点，根据弧相等所对的圆心角相等和弧的度数与它所对圆心角的度数的关系得到∠BAE=∠ABE=15°，则∠DAE=15°，易证△ABE≌△ADE．则BE=DE，∠EDA=∠ABE=15°，得到∠BDE=∠EBD=（180°-30°-30°）÷2=60°，即可判断△BED是等边三角形．

解答：证明：（1）连接OB．如图，
∵AC是⊙O的直径，AB是弦且等于半径长，
∴OA=OB=AB，
∴△AOB为等边三角形，
∴∠OAB=60°，
∵∠BAC=2∠BAN=60°，
∴∠BAN=30°，
∴∠CAN=∠BAC+∠BAN=90°，
即AC⊥MN，
所以MN是⊙O的切线；

（2）连接AE，OE，如图，
∵E是弧AB的中点，
∴∠BAE=∠ABE=15°，
∴∠DAE=15°，
易证△ABE≌△ADE．
∴BE=DE，∠EDA=∠ABE=15°．
∴∠BDE=∠EBD=（180°-30°-30°）÷2=60°．
∴△BDE是等边三角形．

点评：本题考查了切线的判定与性质：过半径的外端点与半径垂直的直线是圆的切线；圆的切线垂直于过切点的半径．也考查了圆周角定理的推论以及三角形全等的判定与性质．