题目内容
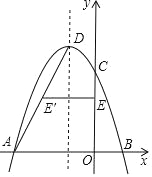
【题目】如图，二次函数y＝﹣
+mx+4﹣m的图象与x轴交于A、B两点（A在B的左侧），与），轴交于点C．抛物线的对称轴是直线x＝﹣2，D是抛物线的顶点．
（1）求二次函数的表达式；
（2）当﹣
＜x＜1时，请求出y的取值范围；
（3）连接AD，线段OC上有一点E，点E关于直线x＝﹣2的对称点E'恰好在线段AD上，求点E的坐标．
【答案】（1）y=﹣
x2﹣2x+6；（2）
＜y＜
；（3）（0，4）．
【解析】
（1）利用对称轴公式求出m的值，即可确定出解析式；
（2）根据x的范围，利用二次函数的增减性确定出y的范围即可；
（3）根据题意确定出D与A坐标，进而求出直线AD解析式，设出E坐标，利用对称性确定出E坐标即可．
（1）∵抛物线对称轴为直线x=﹣2，∴﹣
=﹣2，即m=﹣2，则二次函数解析式为y=﹣x2﹣2x+6；
（2）当x=﹣时，y=；当x=1时，y=．
∵﹣＜x＜1位于对称轴右侧，y随x的增大而减小，∴＜y＜；
（3）当x=﹣2时，y=8，∴顶点D的坐标是（﹣2，8），令y=0，得到：﹣x2﹣2x+6=0，解得：x=﹣6或x=2．
∵点A在点B的左侧，∴点A坐标为（﹣6，0）．
设直线AD解析式为y=kx+b，可得：
，解得：
，即直线AD解析式为y=2x+12．
设E（0，n），则有E′（﹣4，n），代入y=2x+12中得：n=4，则点E坐标为（0，4）．
练习册系列答案
优等生题库系列答案
相关题目
