题目内容
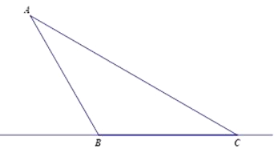
【题目】为保证车辆行驶安全，现在公路旁设立一检测点A观测行驶的汽车是否超速．如图，检测点A到公路的距离是24米，在公路上取两点B、C，使得∠ACB=30°，∠ABC=120°．
(1)求BC的长（结果保留根号）；
(2)已知该路段限速为45千米/小时，若测得某汽车从B到C用时2秒，这辆汽车是否超速？说明理由．（参考数据：
≈1.7，
≈1.4）
【答案】（1）16
（2）超速
【解析】
（1）分别在Rt△ADC与Rt△BDA中，利用正切函数，即可求得CD与BD的长，继而求得BC的长；
（2）由从B到C用时2秒，即可求得这辆校车的速度，比较与45千米/小时的大小，即可确定这辆校车是否超速．
(1)过点A作BC的垂线，垂足即为点D.
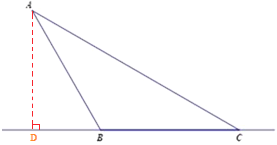
由题意得，AD=24m
在Rt△ADC中，
，
解得
．
在Rt△ABD中，
解得
所以BC=CD-BD=
（米）．
(2)汽车从B到C用时2秒，所以速度为
（米/秒），
因为13.6米/秒=48.96千米/小时>45千米/小时
（或因为45千米/小时=12.5米/秒<13.6米/秒）
所以此汽车超速．
练习册系列答案
相关题目
