Question

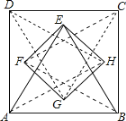
【题目】如图①，∠QPN的顶点P在正方形ABCD两条对角线的交点处，∠QPN=α，∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F（点F与点C、D不重合）．

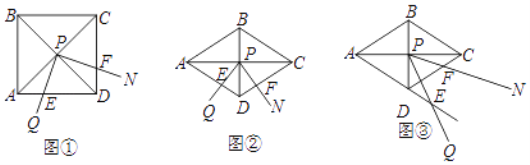
(1)如图①，当α=90°时，求证：DE+DF=AD．

(2)如图②，将图①中的正方形ABCD改为∠ADC=120°的菱形，其他条件不变，当α=60°时，(1)中的结论变为 ，请给出证明．

(3)在(2)的条件下，将∠QPN绕点P旋转，若旋转过程中∠QPN的边PQ与边AD的延长线交于点E，其他条件不变，探究在整个运动变化过程中，DE，DF，AD之间满足的数量关系，直接写出结论，不用加以证明．

Answer 1

【答案】（1）见解析（2）见解析（3）DFDE＝AD．

【解析】

（1）利用正方形的性质得出角与线段的关系，易证得△APE≌△DPF，可得出AE＝DF，即可得出结论DE＋DF＝AD，

（2）取AD的中点M，连接PM，利用菱形的性质，可得出△MDP是等边三角形，易证△MPE≌△FPD，得出ME＝DF，由DE＋ME＝AD，即可得出DE＋DF＝AD，

（3）①当点E落在AD上时，DE＋DF＝AD，②当点E落在AD的延长线上时，DFDE＝AD．

（1）正方形ABCD的对角线AC，BD交于点P，

∴PA＝PD，∠PAE＝∠PDF＝45°，

∵∠APE＋∠EPD＝∠DPF＋∠EPD＝90°，

∴∠APE＝∠DPF，

在△APE和△DPF中

，

∴△APE≌△DPF（ASA），

∴AE＝DF，

∴DE＋DF＝AD；

（2）如图②，取AD的中点M，连接PM，

∵四边形ABCD为∠ADC＝120°的菱形，

∴BD＝AD，∠DAP＝30°，∠ADP＝∠CDP＝60°，

∴△MDP是等边三角形，

∴PM＝PD，∠PME＝∠PDF＝60°，

∵∠PAM＝30°，

∴∠MPD＝60°，

∵∠QPN＝60°，

∴∠MPE＝∠FPD，

在△MPE和△DPF中，

，

∴△MPE≌△DPF（ASA）

∴ME＝DF，

∴DE＋DF＝AD；

（3）如图，

如图③，当点E落在AD的延长线上时，

取AD的中点M，连接PM，

∵四边形ABCD为菱形，∠ADC＝120°，

∴AD＝CD，∠DAP＝30°，AC⊥BD，

∴∠ADP＝∠CDP＝60°，

∵AM＝MD，

∴PM＝MD，

∴△MDP是等边三角形，

∴∠PME＝∠MPD＝60°，PM＝PD，

∵∠QPN＝60°，

∴∠MPE＝∠FPD，

在△MPE和△DPF中，

，

∴△MPE≌△DPF（ASA）．

∴ME＝DF，

∴DFDE＝MEDE＝DM＝AD．