题目内容
【题目】如图,已知平面直角坐标系中,![]() 、
、![]() ,现将线段
,现将线段![]() 绕
绕![]() 点顺时针旋转
点顺时针旋转![]() 得到点
得到点![]() ,连接
,连接![]() .
.
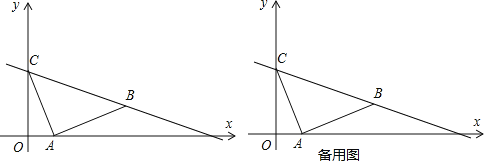
(1)求出直线![]() 的解析式;
的解析式;
(2)若动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 以每分钟
以每分钟![]() 个单位的速度运动,过
个单位的速度运动,过![]() 作
作![]() 交
交![]() 轴于
轴于![]() ,连接
,连接![]() .设运动时间为
.设运动时间为![]() 分钟,当四边形
分钟,当四边形![]() 为平行四边形时,求
为平行四边形时,求![]() 的值.
的值.
(3)![]() 为直线
为直线![]() 上一点,在坐标平面内是否存在一点
上一点,在坐标平面内是否存在一点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为菱形,若存在,求出此时
为顶点的四边形为菱形,若存在,求出此时![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)t=
;(2)t=![]() s时,四边形ABMN是平行四边形;(3)存在,点Q坐标为:
s时,四边形ABMN是平行四边形;(3)存在,点Q坐标为:![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
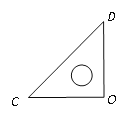
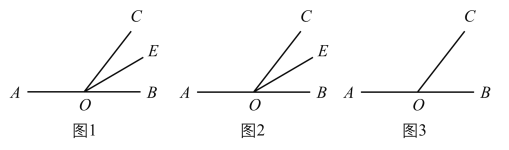
(1)如图1中,作BH⊥x轴于H.证明△COA≌△AHB(AAS),可得BH=OA=1,AH=OC=2,求出点B坐标,再利用待定系数法即可解决问题.
(2)利用平行四边形的性质求出点N的坐标,再求出AN,BM,CM即可解决问题.
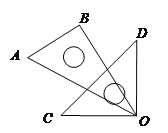
(3)如图3中,当OB为菱形的边时,可得菱形OBQP,菱形OBP1Q1.菱形OBP3Q3,当OB为菱形的对角线时,可得菱形OP2BQ2,点Q2在线段OB的垂直平分线上,分别求解即可解决问题.
(1)如图1中,作BH⊥x轴于H.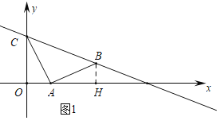
∵A(1,0)、C(0,2),
∴OA=1,OC=2,
∵∠COA=∠CAB=∠AHB=90°,
∴∠ACO+∠OAC=90°,∠CAO+∠BAH=90°,
∴∠ACO=∠BAH,
∵AC=AB,
∴△COA≌△AHB(AAS),
∴BH=OA=1,AH=OC=2,
∴OH=3,
∴B(3,1),
设直线BC的解析式为y=kx+b,则有![]() ,
,
解得: ,
,
∴![]() ;
;
(2)如图2中,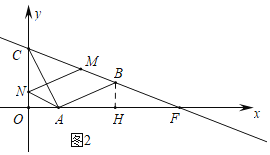
∵四边形ABMN是平行四边形,
∴AN∥BM,
∴直线AN的解析式为:![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵B(3,1),C(0,2),
∴BC=![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴t=![]() s时,四边形ABMN是平行四边形;
s时,四边形ABMN是平行四边形;
(3)如图3中,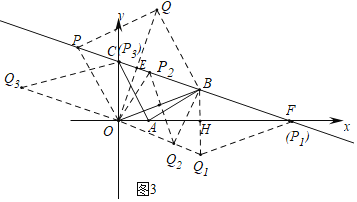
如图3中,当OB为菱形的边时,可得菱形OBQP,菱形OBP1Q1.菱形OBP3Q3,
连接OQ交BC于E,
∵OE⊥BC,
∴直线OE的解析式为y=3x,
由 ,解得:
,解得:![]() ,
,
∴E(![]() ,
,![]() ),
),
∵OE=OQ,
∴Q(![]() ,
,![]() ),
),
∵OQ1∥BC,
∴直线OQ1的解析式为y=-![]() x,
x,
∵OQ1=OB=![]() ,设Q1(m,-
,设Q1(m,-![]() ),
),
∴m2+![]() m2=10,
m2=10,
∴m=±3,
可得Q1(3,-1),Q3(-3,1),
当OB为菱形的对角线时,可得菱形OP2BQ2,点Q2在线段OB的垂直平分线上,
易知线段OB的垂直平分线的解析式为y=-3x+5,
由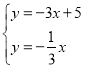 ,解得:
,解得: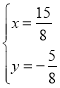 ,
,
∴Q2(![]() ,
,![]() ).
).
综上所述,满足条件的点Q坐标为:![]() 或
或![]() 或
或![]() 或
或![]() .
.

【题目】弹簧挂上物体后会伸长,已知一弹簧的长度(cm)与所挂物体的质量(kg)之间的关系如表所示.
所挂物体的质量 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
弹簧的长度 | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 | 15 | 15.5 |
(1)上表反映了哪些变量之间的关系?哪个是自变量,哪个是因变量?
(2)当物体的质量为2kg时,弹簧的长度是多少?
(3)当物体的质量逐渐增加时,弹簧的长度怎样变化?
(4)如果物体的质量为xkg,弹簧的长度为ycm,根据上表写出y与x的关系式;
(5)当物体的质量为2.5kg时,根据(4)的关系式,求弹簧的长度.