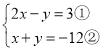题目内容
【题目】如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
(1)当∠BQD=30°时,求AP的长;
(2)当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.

【答案】(1)2(2)当点P、Q运动时,线段DE的长度不会改变。理由见解析
【解析】解:(1)∵△ABC是边长为6的等边三角形,∴∠ACB=60°。
∵∠BQD=30°,∴∠QCP=90°。
设AP=x,则PC=6﹣x,QB=x,∴QC=QB+C=6+x。
∵在Rt△QCP中,∠BQD=30°,∴PC=![]() QC,即6﹣x=
QC,即6﹣x=![]() (6+x),解得x=2。
(6+x),解得x=2。
∴当∠BQD=30°时,AP=2。
(2)当点P、Q运动时,线段DE的长度不会改变。理由如下:
作QF⊥AB,交直线AB的延长线于点F,连接QE,PF。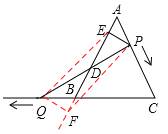
∵PE⊥AB于E,∴∠DFQ=∠AEP=90°。
∵点P、Q做匀速运动且速度相同,∴AP=BQ。
∵△ABC是等边三角形,∴∠A=∠ABC=∠FBQ=60°。
∴在△APE和△BQF中,
∵∠A=∠FBQ,AP=BQ,∠AEP=∠BFQ=90°,∴△APE≌△BQF(AAS)。
∴AE=BF,PE=QF且PE∥QF。∴四边形PEQF是平行四边形。
∴DE=![]() EF。
EF。
∵EB+AE=BE+BF=AB,∴DE=![]() AB。
AB。
又∵等边△ABC的边长为6,∴DE=3。
∴当点P、Q运动时,线段DE的长度不会改变。
(1)由△ABC是边长为6的等边三角形,可知∠ACB=60°,再由∠BQD=30°可知∠QCP=90°,设AP=x,则PC=6﹣x,QB=x,在Rt△QCP中,∠BQD=30°,PC=![]() QC,即6﹣x=
QC,即6﹣x=![]() (6+x),求出x的值即可。
(6+x),求出x的值即可。
(2)作QF⊥AB,交直线AB的延长线于点F,连接QE,PF,由点P、Q做匀速运动且速度相同,可知AP=BQ,再根据全等三角形的判定定理得出△APE≌△BQF,再由AE=BF,PE=QF且PE∥QF,可知四边形PEQF是平行四边形,进而可得出EB+AE=BE+BF=AB,DE=![]() AB,由等边△ABC的边长为6可得出DE=3,故当点P、Q运动时,线段DE的长度不会改变。
AB,由等边△ABC的边长为6可得出DE=3,故当点P、Q运动时,线段DE的长度不会改变。

 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案【题目】为了比较市场上甲、乙两种电子钟每日走时误差的情况,从这两种电子钟中,各随机抽取10台进行测试,两种电子钟走时误差的数据如下表(单位:秒):
编号 类型 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | 九 | 十 |
甲种电子钟 | 1 | -3 | -4 | 4 | 2 | -2 | 2 | -1 | -1 | 2 |
乙种电子钟 | 4 | -3 | -1 | 2 | -2 | 1 | -2 | 2 | -2 | 1 |
(1) 计算甲、乙两种电子钟走时误差的平均数;
(2) 计算甲、乙两种电子钟走时误差的方差;
(3) 根据经验,走时稳定性较好的电子钟质量更优.若两种类型的电子钟价格相同,请问:你买哪种电子钟?为什么?
【题目】小明同学在用描点法画二次函数y=ax2+bx+c图象时,由于粗心,他算错了一个y值,列出了下面表格:
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y=ax2+bx+c | … | 5 | 3 | 2 | 3 | 6 | … |
(1)请指出这个错误的y值,并说明理由;
(2)若点M(a,y1),N(a+4,y2)在二次函数y=ax2+bx+c图象上,且a>﹣1,试比较y1与y2的大小.