Question

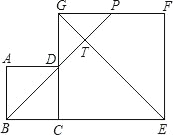
【题目】如图，在△ABC中，∠ACB＝90°，AC＝BC，点E是BC上一点（不与点B，C重合），点M是AE上一点（不与点A，E重合），连接并延长CM交AB于点G，将线段CM绕点C按顺时针方向旋转90°，得到线段CN，射线BN分别交AE的延长线和GC的延长线于D，F．

（1）求证：△ACM≌△BCN；

（2）求∠BDA的度数；

（3）若∠EAC＝15°，∠ACM＝60°，AC＝+1，求线段AM的长．

Answer 1

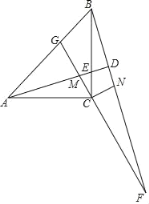
【答案】（1）见解析；（2）∠BDA＝90°；（3）AM＝．

【解析】

（1）根据题意可知∠ACM＝∠BCN，再利用SAS即可证明

（2）根据（1）可求出∠ACE＝∠BDE＝90°，即可解答

（3）作MH⊥AC交AC于H．在AC上取一点，使得AQ＝MQ，设EH＝a．可知AQ＝QM＝2a，QH＝ a，再求出a的值，利用勾股定理即可解答

（1）∵∠ACB＝90°，∠MCN＝90°，

∴∠ACM＝∠BCN，

在△MAC和△NBC中

，

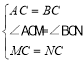∴△MAC≌△NBC（SAS）．

（2）∵△MAC≌△NBC，

∴∠NBC＝∠MAC

∵∠AEC＝∠BED，

∴∠ACE＝∠BDE＝90°，

∴∠BDA＝90°．

（3）作MH⊥AC交AC于H．在AC上取一点，使得AQ＝MQ，设EH＝a．

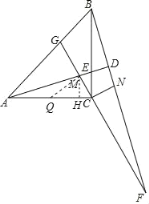
∵AQ＝QM，

∴∠QAE＝∠AMQ＝15°，

∴∠EQH＝30°，

∴AQ＝QM＝2a，QH＝ a，

∵∠ECH＝60°，

∴CH＝ a，

∵AC＝+1，

∴2a+a+a＝+1，

∴a＝ ，

∵AM＝ ＝（ + ）a＝．