题目内容
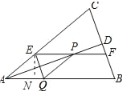
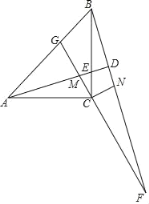
【题目】如图,在△ABC中,AB=AC,AD平分∠BAC交BC于点D,在线段AD上任到一点P(点A除外),过点P作EF∥AB,分别交AC、BC于点E、F,作PQ∥AC,交AB于点Q,连接QE与AD相交于点G.
(1)求证:四边形AQPE是菱形.
(2)四边形EQBF是平行四边形吗?若是,请证明;若不是,请说明理由.
(3)直接写出P点在EF的何处位置时,菱形AQPE的面积为四边形EQBF面积的一半.

【答案】(1)见解析;(2)结论:四边形EQBF是平行四边形.见解析;(3)当P为EF中点时,S菱形AEPQ=![]() S四边形EFBQ.
S四边形EFBQ.
【解析】
(1)先证出四边形AEPQ为平行四边形,关键是找一组邻边相等,由AD平分∠BAC和PE∥AQ可证∠EAP=∠EPA,得出AE=EP,即可得出结论;
(2)只要证明EQ∥BC,EF∥AB即可;
(3)S菱形AEPQ=EPh,S平行四边形EFBQ=EFh,若菱形AEPQ的面积为四边形EFBQ面积的一半,则EP=![]() EF,因此P为EF中点时,S菱形AEPQ=
EF,因此P为EF中点时,S菱形AEPQ=![]() S四边形EFBQ.
S四边形EFBQ.
(1)证明:∵EF∥AB,PQ∥AC,
∴四边形AEPQ为平行四边形,
∴∠BAD=∠EPA,
∵AB=AC,AD平分∠CAB,
∴∠CAD=∠BAD,
∴∠CAD=∠EPA,
∴EA=EP,
∴四边形AEPQ为菱形.
(2)解:结论:四边形EQBF是平行四边形.
∵四边形AQPE是菱形,
∴AD⊥EQ,即∠AGQ=90°,
∵AB=AC,AD平分∠BAC,
∴AD⊥BC即∠ADB=90°,
∴EQ∥BC
∵EF∥QB,
∴四边形EQBF是平行四边形.
(3)解:当P为EF中点时, S菱形AEPQ=![]() S四边形EFBQ
S四边形EFBQ
∵四边形AEPQ为菱形,
∴AD⊥EQ,
∵AB=AC,AD平分∠BAC,
∴AD⊥BC,
∴EQ∥BC,
又∵EF∥AB,
∴四边形EFBQ为平行四边形.
作EN⊥AB于N,如图所示:
∵P为EF中点
则S菱形AEPQ=EPEN=![]() EFEN=
EFEN=![]() S四边形EFBQ.
S四边形EFBQ.