题目内容
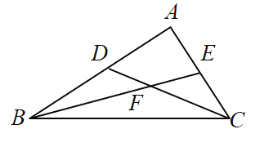
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 中点,
中点,![]() 为
为![]() 上一点(不与点
上一点(不与点![]() 、
、![]() 重合),连接
重合),连接![]() 、
、![]() 交于点
交于点![]() ,
,![]() .设
.设![]() ,
,![]() .则
.则![]() 关于
关于![]() 的函数解析式为_______.
的函数解析式为_______.
【答案】![]()
【解析】
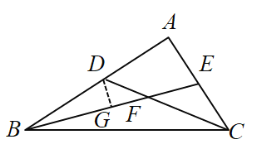
过D点作DG⊥AB交BE与G,再通过说明△DGF为等腰三角形得到DG=GF;然后再说明DG=GF=![]() (4-x),G为BE的中点;再通过证明△EFC为等腰三角形得到EF=EC,进一步说明
(4-x),G为BE的中点;再通过证明△EFC为等腰三角形得到EF=EC,进一步说明
AE=2EG=4+x,最后运用勾股定理解答即可.
过D点作DG⊥AB交BE与G,
∴∠FDG+∠ADC=90°
又∵∠DFB+∠ADC=90°
∴∠FDG=∠DFB
∴△DGF为等腰三角形,
∴DG=GF
又∵在Rt△ABE中D为AB的中点,
∴DG为△ABE的中位线
∴DG=GF=![]() AE=
AE=![]() (4-x),G为BE的中点
(4-x),G为BE的中点
又∵在RT△ADC中∠ADC+∠ACD=90°
∴∠ACD=∠DFB
又∵∠DFB=∠EFC
∴∠ACD=∠EFC
∴△EFC为等腰三角形
∴EF=EC
∴EG=EF+GF=DG+EC=2+![]() x
x
∴BE=2EG=4+x
又∵△ABE为直角三角形
∴由勾股定理可的AB=![]()
∴![]()

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案【题目】今年疫情防控期间,我市一家服装有限公司生产了一款服装,为对比分析以前实体商店和现在网上商店两种途径的销售情况,进行了为期30天的跟踪调查.其中实体商店的日销售量![]() (百件)与时间
(百件)与时间![]() (
(![]() 为整数,单位:天)的部分对应值如下表所示;网上商店的日销售量
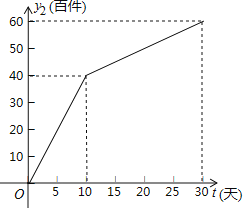
为整数,单位:天)的部分对应值如下表所示;网上商店的日销售量![]() (百件)与时间
(百件)与时间![]() (
(![]() 为整数,单位:天)的关系如图所示.
为整数,单位:天)的关系如图所示.
时间 | 0 | 6 | 10 | 12 | 18 | 20 | 24 | 30 |
日销售量 | 0 | 72 | 100 | 108 | 108 | 100 | 72 | 0 |
(1)请你在一次函数、二次函数和反比例函数中,选择合适的函数反映![]() 与
与![]() 的变化规律,并求出
的变化规律,并求出![]() 与
与![]() 的函数关系式及自变量
的函数关系式及自变量![]() 的取值范围;
的取值范围;
(2)求![]() 与
与![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)在跟踪调查的30天中,设实体商店和网上商店的日销售总量为![]() (百件),求
(百件),求![]() 与
与![]() 的函数关系式;当
的函数关系式;当![]() 为何值时,日销售量
为何值时,日销售量![]() 达到最大,并求出此时的最大值.
达到最大,并求出此时的最大值.