题目内容
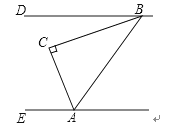
【题目】如图,∠CAB+∠ABC=90°,AD平分∠CAB,与BC边交于点D,BE平分∠ABC与AC边交于点E。
(1)依题意补全图形,并猜想∠DAB+∠EBA的度数等于__________;
(2)证明以上结论。
证明:∵ AD平分∠CAB,BE平分∠ABC,
∴∠DAB=![]() ∠CAB,
∠CAB,
∠EBA=__________.
(理由:____________________)
∵∠CAB+∠ABC=90°,
∴∠DAB+∠EBA=______×(∠______+∠______)=______。
【答案】图像见详解;45![]()
![]() ∠CBA; 角平方线的定义
∠CBA; 角平方线的定义 ![]() CAB ABC 45°
CAB ABC 45°
【解析】
(1)根据题意画出图形,然后由角平分线的定义可求得∠DAB+∠EBA =45![]() ;
;
(2)根据角平分线的定义以及证明过程进行填写即可.
(1)解:如图所示: 
猜想∠DAB+∠EBA =45![]() .
.
(2)证明: 证明:∵ AD平分∠CAB,BE平分∠ABC,
∴∠DAB=![]() ∠CAB,
∠CAB,
∠EBA=![]() ∠CBA.
∠CBA.
(理由:角平方线的定义)
∵∠CAB+∠ABC=90°,
∴∠DAB+∠EBA=![]() ×(∠CAB +∠ABC)=45°.
×(∠CAB +∠ABC)=45°.
故答案:![]() ∠CAB;角平方线的定义;
∠CAB;角平方线的定义;![]() ;CAB ;ABC;45°.
;CAB ;ABC;45°.

练习册系列答案
相关题目
【题目】研究问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球,怎样估算不同颜色球的数量? 操作方法:先从盒中摸出8个球,画上记号放回盒中,再进行摸球实验,摸球实验的要求:先搅拌均匀,每次摸出一个球,放回盒中,再继续.
活动结果:摸球实验活动一共做了50次,统计结果如下表:
球的颜色 | 无记号 | 有记号 | ||
红色 | 黄色 | 红色 | 黄色 | |
摸到的次数 | 18 | 28 | 2 | 2 |
推测计算:由上述的摸球实验可推算:
(1)盒中红球、黄球各占总球数的百分比分别是多少?
(2)盒中有红球多少个?