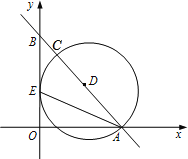题目内容
【题目】已知:![]() 、
、![]() 是圆
是圆![]() 中的两条弦,连接
中的两条弦,连接![]() 交
交![]() 于点
于点![]() ,点
,点![]() 在
在![]() 上,连接
上,连接![]() ,
,![]() .
.
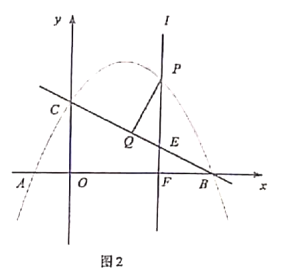
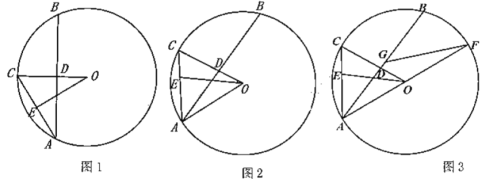
(1)如图1,若![]() ,求证:弧
,求证:弧![]()
![]() 弧
弧![]() ;
;
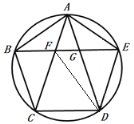
(2)如图2,连接![]() ,若
,若![]() ,求证:
,求证:![]() ;
;
(3)如图3,在第(2)问的条件下,延长![]() 交圆
交圆![]() 于点
于点![]() ,点
,点![]() 在
在![]() 上,连接
上,连接![]() ,若
,若![]() ,
,![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)通过角度之间的关系,求得![]() ,得证
,得证![]() ,即可证明
,即可证明![]()
![]()
![]() ;
;
(2)通过证明![]() ≌
≌![]() ,求得
,求得![]() ,
,![]() ,可得
,可得![]() 为等边三角形,可得
为等边三角形,可得![]() ,
,![]() ,即可证明
,即可证明![]() ;
;
(3)延长![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 到点
到点![]() ,使
,使![]() ,连接
,连接![]() ,
,![]() ,设
,设![]() ,先证明
,先证明![]() ≌
≌![]() ,可得
,可得![]() ,设
,设![]() ,解
,解![]() 得
得![]() ,
,![]() ,过点
,过点![]() 作
作![]() ,在
,在![]() 中,解得
中,解得![]() ,故在
,故在![]() 中,
中,![]() ,解得
,解得![]() ,即可求出线段BG的长度.
,即可求出线段BG的长度.
(1)证明:
∵![]() ,
,![]()
∴![]()
∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
![]()
![]()
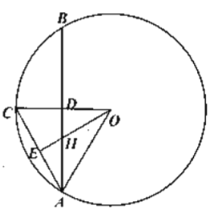
(2)证明:
∵![]() ,
,![]()
∵![]()
∴![]()
在![]() 和
和![]() 中
中
∵![]() ,
,![]() ,
,![]()
∴![]() ≌
≌![]()
∴![]() ,
,![]()
∴![]()
∴![]() 为等边三角形
为等边三角形
∵![]() ,
,![]()
∴![]()
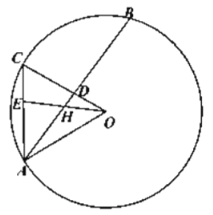
(3)证明:延长![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 到点
到点![]() ,使
,使![]() ,连接
,连接![]() ,
,![]()
设![]() ,
,
∴![]()
∵![]() ,
, ![]()
∴![]()
∴![]()
∵![]()
∴![]()
在![]() 和
和![]() 中
中
∵![]() ,
, ![]() ,
, ![]()
∴![]() ≌
≌![]()
∴![]()
∵![]()
∴![]()
∴![]()
设![]() ,
,
∴![]() ,
,![]() ,
,![]()
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]()
解![]() 得
得![]() ,
,![]()
过点![]() 作
作![]() ,在
,在![]() 中,
中,
∵![]() ,
,![]()
∴![]() ,
,![]() ,
,![]()
在![]() 中,
中,![]() ,
,![]()
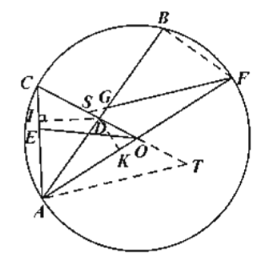

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目