题目内容
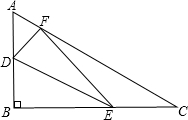 如图所示,已知Rt△ABC中,∠B=90°,AB=3,BC=4,D,E,F分别是三边AB,BC,CA上的点,则DE+EF+FD的最小值为
如图所示,已知Rt△ABC中,∠B=90°,AB=3,BC=4,D,E,F分别是三边AB,BC,CA上的点,则DE+EF+FD的最小值为
- A.

- B.
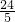
- C.5
- D.6
B
分析:作F关于AB、BC的对称点F′、F″,作AC关于AB、BC的对称线段,可以发现F′,F″是一个菱形对边上的关于中心B对称的对称点.容易发现,F′F″的最短距离就是菱形对边的距离,也就是菱形的高.根据菱形的性质即可求出DE+EF+FD的最小值.
解答: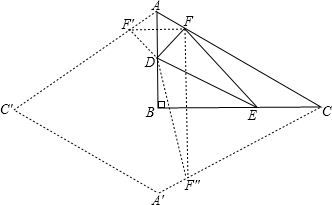 解:作F关于AB、BC的对称点F′、F″
解:作F关于AB、BC的对称点F′、F″
则FD=F′D,FE=F″E.
DE+EF+FD=DE+F′D+F″E.
两点之间线段最短,可知当F固定时,DE+F′D+F″E的最小值就是线段F′F″的长.
于是问题转化:F运动时,F′F″什么时候最短.
F′,F″是关于B点对称的.
作AC关于AB、BC的对称线段,可以发现F′,F″是一个菱形对边上的关于中心B对称的对称点.
很容易发现,F′F″的最短距离就是菱形对边的距离,也就是菱形的高.
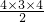 =5x
=5x
x=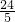 ,高是
,高是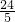 ,
,
故DE+EF+FD的最小值为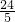 ,
,
此时F在斜边上的高的垂足点,D、E在B点.
点评:本题考查菱形的判定和性质及轴对称--最短路线问题的综合应用,有一定的难度.关键是确定F在斜边上的高的垂足点,D、E在B点.
分析:作F关于AB、BC的对称点F′、F″,作AC关于AB、BC的对称线段,可以发现F′,F″是一个菱形对边上的关于中心B对称的对称点.容易发现,F′F″的最短距离就是菱形对边的距离,也就是菱形的高.根据菱形的性质即可求出DE+EF+FD的最小值.
解答:
 解:作F关于AB、BC的对称点F′、F″
解:作F关于AB、BC的对称点F′、F″则FD=F′D,FE=F″E.
DE+EF+FD=DE+F′D+F″E.
两点之间线段最短,可知当F固定时,DE+F′D+F″E的最小值就是线段F′F″的长.
于是问题转化:F运动时,F′F″什么时候最短.
F′,F″是关于B点对称的.
作AC关于AB、BC的对称线段,可以发现F′,F″是一个菱形对边上的关于中心B对称的对称点.
很容易发现,F′F″的最短距离就是菱形对边的距离,也就是菱形的高.
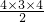 =5x
=5xx=
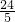 ,高是
,高是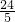 ,
,故DE+EF+FD的最小值为
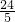 ,
,此时F在斜边上的高的垂足点,D、E在B点.
点评:本题考查菱形的判定和性质及轴对称--最短路线问题的综合应用,有一定的难度.关键是确定F在斜边上的高的垂足点,D、E在B点.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
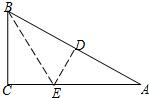 B边上的点D、要使点D恰为AB的中点,问在图中还要添加什么条件?(直接填写答案)
B边上的点D、要使点D恰为AB的中点,问在图中还要添加什么条件?(直接填写答案)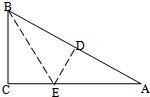 17、如图所示,已知Rt△ABC中,∠C=90°,沿过B点的一条直线BE折叠这个三角形,使C点落在AB边上的点D.要使点D恰为AB的中点,问在图中还要添加什么条件?(直接填写答案)
17、如图所示,已知Rt△ABC中,∠C=90°,沿过B点的一条直线BE折叠这个三角形,使C点落在AB边上的点D.要使点D恰为AB的中点,问在图中还要添加什么条件?(直接填写答案) 22、如图所示,已知Rt△ABC中,AB=AC,BD平分∠ABC,CE⊥BD交BD延长线于E,BA、CE延长线相交于F点.
22、如图所示,已知Rt△ABC中,AB=AC,BD平分∠ABC,CE⊥BD交BD延长线于E,BA、CE延长线相交于F点.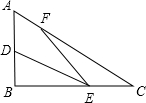 如图所示,已知Rt△ABC中,∠B=90°,AB=3,BC=4,D、E、F分别是三边AB、BC、AC上的点,则DE+EF+FD的最小值为
如图所示,已知Rt△ABC中,∠B=90°,AB=3,BC=4,D、E、F分别是三边AB、BC、AC上的点,则DE+EF+FD的最小值为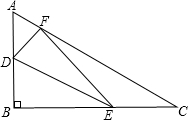 如图所示,已知Rt△ABC中,∠B=90°,AB=3,BC=4,D,E,F分别是三边AB,BC,CA上的点,则DE+EF+FD的最小值为( )
如图所示,已知Rt△ABC中,∠B=90°,AB=3,BC=4,D,E,F分别是三边AB,BC,CA上的点,则DE+EF+FD的最小值为( )