题目内容
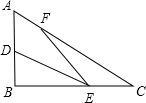如图所示，已知Rt△ABC中，∠B=90°，AB=3，BC=4，D、E、F分别是三边AB、BC、AC上的点，则DE+EF+FD的最小值为分析：根据轴对称的性质和两点之间线段最短的性质来计算．
解答：
解：如图，由勾股定理知，AC=5，
作出△ABC关于AB对称的△ABG，△ABC关于AC对称的△ACH，
则点E关于AB的对称点为S，
关于AC的对称点为W，
当S，D，F，W在同一直线上，且点S与点E重合在点B，
点W在点H时，DE+EF+FD有最小值，根
据三角形的面积公式可求得AC边上的高为
，
故DE+EF+FD的最小值=2×
=
．
解：如图，由勾股定理知，AC=5，作出△ABC关于AB对称的△ABG，△ABC关于AC对称的△ACH，
则点E关于AB的对称点为S，
关于AC的对称点为W，
当S，D，F，W在同一直线上，且点S与点E重合在点B，
点W在点H时，DE+EF+FD有最小值，根
据三角形的面积公式可求得AC边上的高为
| 12 |
| 5 |
故DE+EF+FD的最小值=2×
| 12 |
| 5 |
| 24 |
| 5 |
点评：本题利用了轴对称图形的性质和两点之间线段最短的性质求解．
练习册系列答案
相关题目
B边上的点D、要使点D恰为AB的中点，问在图中还要添加什么条件？（直接填写答案）
17、如图所示，已知Rt△ABC中，∠C=90°，沿过B点的一条直线BE折叠这个三角形，使C点落在AB边上的点D．要使点D恰为AB的中点，问在图中还要添加什么条件？（直接填写答案）
22、如图所示，已知Rt△ABC中，AB=AC，BD平分∠ABC，CE⊥BD交BD延长线于E，BA、CE延长线相交于F点．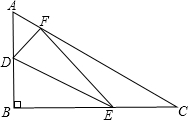
如图所示，已知Rt△ABC中，∠B=90°，AB=3，BC=4，D，E，F分别是三边AB，BC，CA上的点，则DE+EF+FD的最小值为（ ）