��Ŀ����
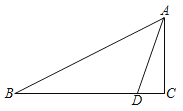
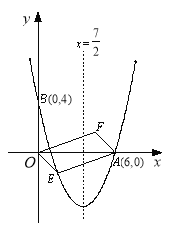
����Ŀ����1����ͼ1������ABCD���������߳�Ϊ1�������ι��ɣ������������ƴ��һ�������ABCD�����ȵ������Σ�
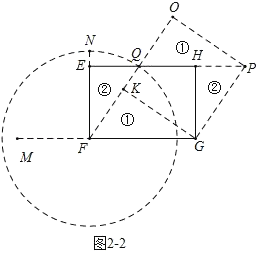
��2����ͼ2������EFGH�ij�FGΪ6����EFΪ4���ü��������Σ�Ȼ����ƴ�ӳ�һ�������EFGH�����ȵ������Σ������ü���ƴ�Ӻ��ͼ�Σ���Ҫ˵���ü��������ȷ���ģ������û���뵽�÷��������ü��������Ӧ�ԣ�ϸ��������ѧ��ʵ�����������а�����
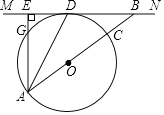
��3����ͼ3���ڡ�O�У�MNΪֱ����PQ��MN������Ϊ��Q������O�ڵ�P������PM��PN����֤��PQ2��MQNQ���˽��ۿ�ֱ�����ã�
���𰸡���1������������2������������3��������
��������
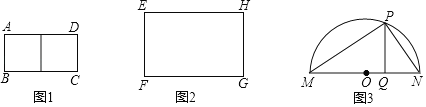
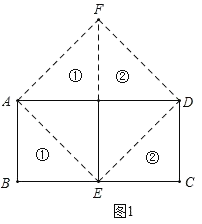
��1����ͼ1��ʾ���ֱ���AE��DE����һ��������ƴ����ԭ���������ȵ�������AEDF��
��2����ͼ2��1���ӳ�GF��M��ʹMF��EF��4������MGΪֱ����Բ���ӳ�FE��Բ�ڵ�N����![]() ��֪NF2��MFGF��EFGF��24����ͼ2��2����FΪԲ�ģ�FNΪ�뾶��Բ��������EH���ڵ�Q����G��GK��FQ�ڵ�K����FQ��GK�������ƴ��������KGPO����S������KGPO��24��
��֪NF2��MFGF��EFGF��24����ͼ2��2����FΪԲ�ģ�FNΪ�뾶��Բ��������EH���ڵ�Q����G��GK��FQ�ڵ�K����FQ��GK�������ƴ��������KGPO����S������KGPO��24��
��1����ͼ1��ʾ���ֱ���AE��DE����һ��������ƴ����ԭ���������ȵ�������AEDF��
��2����ͼ2��1���ӳ�GF��M��ʹMF��EF��4������MGΪֱ����Բ���ӳ�FE��Բ�ڵ�N��
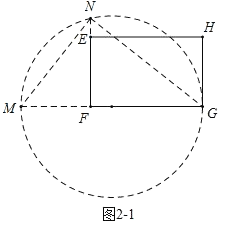
���MNG=90��
���GNF+��MNF=90��,
�ߡ�NFM=90��,
���NMF+��MNF=90��,
���NMF=��GNF,
�֡�NFM=��NFG,
��![]()
��![]()
��NF2��MFGF��EFGF��24��
��S��������S������24��
��ͼ2��2����FΪԲ�ģ�FNΪ�뾶��Բ��������EH���ڵ�Q����G��GK��FQ�ڵ�K��
��FQ��GK�������ƴ��������KGPO����S������KGPO��24��