题目内容
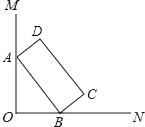
【题目】如图,A(﹣5,0),B(﹣3,0)点C在y的正半轴上,∠CBO=45°,CD∥AB.∠CDA=90°,点P从点A出发,沿x轴向右以每秒1个单位长度的速度运动,运动时间为t秒.
(1)当时t=1,求PC的长;
(2)当∠BCP=15°时,求t的值;
(3)以线段PC为直径的⊙Q随点P的运动而变化,当⊙Q与四边形ABCD的边(或边所在的直线)相切时,求t的值.

【答案】(1)PC=5;(2)当∠BCP=15°时,t的值为(5﹣3![]() )秒或(5﹣
)秒或(5﹣![]() )秒;(3)t的值为8秒或5秒或
)秒;(3)t的值为8秒或5秒或![]() 秒.
秒.
【解析】
(1)由题意可知△BOC是等腰直角三角形,由此即可解决问题.
(2)分两种情形①当点P在点B右侧时,②当点P′在点B左侧时,分别解直角三角形即可.
(3)由题意知,若该圆与四边形ABCD的边相切,有三种情况:①当该圆与BC相切于点C时.②当该圆与CD相切于点C时.③当该圆与AD相切时;分别解直角三角形,求出AP的长即可解决问题.
(1)A(﹣5,0),B(﹣3,0),
∴OA=5,OB=3,
当t=1时,AP=1,
∴OP=OA﹣AP=4,
∵∠CBO=45°,∠BOC=90°,
∴△BOC是等腰直角三角形,
∴∠OCB=45°,OC=OB=3,
∴PC=![]() =5;
=5;
(2)分两种情况:如图1所示:①当P在点B的左侧时,
∵∠CBO=45°,∠BCP=15°
∴∠OCP=∠OCB+∠BCP=45°+15°=60°,
∴∠OPC=30°,
∴OP=![]() OC=3
OC=3![]() ,
,
∴AP=OA﹣OP=5﹣3![]() ,
,
∵点P沿x轴向右以每秒1个单位的速度运动,
∴t=5﹣3![]() ,
,
②当![]() 在点B的右侧时,
在点B的右侧时,
∵∠OCB=45°,∠BC![]() =15°
=15°
∴∠OC![]() =∠OCB﹣∠BC
=∠OCB﹣∠BC![]() =45°﹣15°=30°,
=45°﹣15°=30°,
∴O![]() =
=![]() OC=
OC=![]() ,
,
∴A![]() =OA﹣O
=OA﹣O![]() =5﹣
=5﹣![]() ,
,
∵点![]() 沿x轴向右以每秒1个单位的速度运动,
沿x轴向右以每秒1个单位的速度运动,
∴t=5﹣![]() ;
;
综上所述,当∠BCP=15°时,t的值为(5﹣3![]() )秒或(5﹣
)秒或(5﹣![]() )秒;
)秒;
(3)如图2中,由题意知,若该圆与四边形ABCD的边相切,有以下三种情况:
①当该圆与BC相切于点C时,有∠BCP=90°,
从而∠OCP=45°,得到OP1=OC=3,此时AP1=5+3=8,
∴t=8;
②当该圆与CD相切于点C时,有P2C⊥CD,即点P2与点O重合,
此时AP2=5,
∴t=5;
③当该圆与AD相切时,
设P3(5﹣t,0),则Q(![]() ,
,![]() ),半径r2=(
),半径r2=(![]() )2+(
)2+(![]() )2,
)2,
作QH⊥AD于点H,则QH=![]() ,
,
∵QH2=r2,
∴(![]() )2=(
)2=(![]() )2+(
)2+(![]() )2,
)2,
解得t=![]() ,
,
综上所述,t的值为8秒或5秒或![]() 秒.
秒.



【题目】初一(1)班针对“你最喜爱的课外活动项目”对全班学生进行调查(每名学生分别选一个活动项目),并根据调查结果列出统计表,绘制成扇形统计图.
男、女生所选项目人数统计表
项目 | 男生(人数) | 女生(人数) |
机器人 | 7 | 9 |
3D打印 | m | 4 |
航模 | 2 | 2 |
其他 | 5 | n |
根据以上信息解决下列问题:
(1)m= ,n= ;
(2)扇形统计图中机器人项目所对应扇形的圆心角度数为 °;
(3)从选航模项目的4名学生中随机选取2名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的2名学生中恰好有1名男生、1名女生的概率.