题目内容
【题目】已知:关于x的一元二次方程mx2﹣3(m﹣1)x+2m﹣3=0(m>3).
(1)求证:方程总有两个不相等的实数根;
(2)设方程的两个实数根分别为x1 , x2(用含m的代数式表示);
①求方程的两个实数根x1 , x2(用含m的代数式表示);
②若mx1<8﹣4x2 , 直接写出m的取值范围.
【答案】
(1)证明:∵mx2﹣3(m﹣1)x+2m﹣3=0(m>3)是关于x的一元二次方程,
∴△=[(﹣3(m﹣1)]2﹣4m(2m﹣3)=m2﹣6m+9=(m﹣3)2,
∵m>3,
∴(m﹣3)2>0,即△>0,
∴方程总有两个不相等的实数根
(2)①由求根公式得x= ![]() ,
,
∴x=1,或x= ![]() ,
,
∵m>3,
∴ ![]() >3,
>3,
当x1<x2,
∴x1=1,x2=2﹣ ![]() ;
;
当x1>x2,
这种情况不存在;
∴x1=1,x2=2﹣ ![]() ;
;
②∵mx1<8﹣4x2,
∴m<8﹣4(2﹣ ![]() ),
),
解得:3<m<2 ![]() .
.
【解析】(1)由于m>3,此方程为关于x的一元二次方程,再计算出判别式△=(m﹣3)2 , 然后根据判别式的意义即可得到结论;(2)②由求根公式得到x=1,或x= ![]() ,即可得到结论;②根据mx1<8﹣4x2 , 即可得到 结果.
,即可得到结论;②根据mx1<8﹣4x2 , 即可得到 结果.
【考点精析】根据题目的已知条件,利用求根公式和根与系数的关系的相关知识可以得到问题的答案,需要掌握根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根;一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商.

【题目】为了让同学们了解自己的体育水平,初二1班的体育康老师对全班45名学生进行了一次体育模拟测试(得分均为整数)成绩满分为10分,成绩达到9分以上(包含9分)为优秀,成绩达到6分以上(包含6分)为合格,1班的体育委员根据这次测试成绩,制作了统计图和分析表如下: 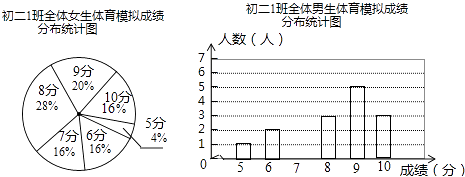
初二1班体育模拟测试成绩分析表
平均分 | 方差 | 中位数 | 众数 | 合格率 | 优秀率 | |
男生 | 2 | 8 | 7 | 95% | 40% | |
女生 | 7.92 | 1.99 | 8 | 96% | 36% |
根据以上信息,解答下列问题:
(1)在这次测试中,该班女生得10分的人数为4人,则这个班共有女生人;
(2)补全初二1班男生体育模拟测试成绩统计图,并把相应的数据标注在统计图上;
(3)补全初二1班体育模拟测试成绩分析表;
(4)你认为在这次体育测试中,1班的男生队、女生队哪个表现更突出一些?并写出一条支持你的看法的理由;
(5)体育康老师说,从整体看,1班的体育成绩在合格率方面基本达标,但在优秀率方面还不够理想,因此他希望全班同学继续加强体育锻炼,争取在期末考试中,全班的优秀率达到60%,若男生优秀人数再增加6人,则女生优秀人数再增加多少人才能完成康老师提出的目标?